1. 零向量
零向量每一维都是零，大小为零没有标的目的
2. 向量的大小（模）1.向量的模的概念 所谓的向量的模就是指向量的大小或者说长度。
2.向量的模的运算法例
在线性代数中，向量的模凡是用在向量两边各加两条竖线的体例暗示，如||v||，暗示向量v的模。向量的模的计算公式如下：
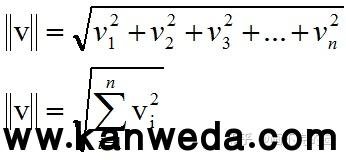
关于2D，3D向量的如下
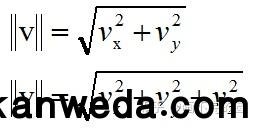3. 尺度化向量
关于许多向量，我们不需要存眷它的大小只需要关心它的标的目的，那种情况下利用单元向量将会十分便利。单元向量就是大小为1的向量，单元向量也被称为尺度化向量。 关于肆意非零向量v，都能计算出一个和v标的目的不异的单元向量n，那个过程被称做为向量的“尺度化”，要尺度化向量，将向量除以它的大小（模）即可。
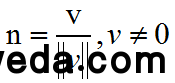4.向量加减法
1.向量的加法和减法的前提
若是两个向量的维数不异，那么他们可以相加减，运算成果的向量的维数和原向量不异。
2.运算法例
向量的加法等于两个向量的重量相加，向量的减法相当于加上一个负向量。
5. 向量点乘
定义 向量点乘又被称为内积，即每个维度成就的和。
几何解释 点乘的成果描述了两个向量的类似水平，点乘成果越大，两个向量月类似。 点乘等于向量大小与向量夹角的cos值的乘积；
向量投影
投影
法线
6. 向量的叉乘
1.根本概念
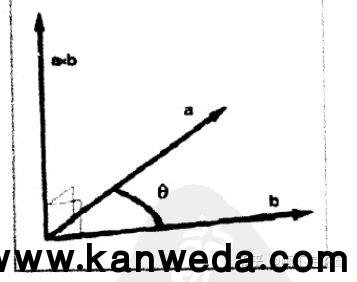
两个向量的叉乘得到是向量，且那个向量垂曲于本来的两个向量。向量的叉乘只能够运用在3D向量中。
2.数学运算公式
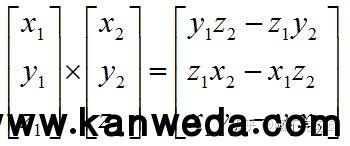
3.几何运算公式
向量叉乘的成果向量的长度与两个向量的夹角有关，且成正弦函数关系，若是向量a和b是平行关系，则叉乘的成果为0，因为sin0为0
4.向量叉乘标的目的的判断
向量的叉乘是通过右手定章来判断成果向量的标的目的的。伸出右手，四指弯曲契合向量叉乘的挨次，那么大拇指就是叉乘后成果向量的标的目的。如下图axb，右手四指弯曲标的目的从a到b，大拇指标的目的向上就是叉乘成果向量的标的目的。
