向量的计算:
1、向量的定义:
·向量是有大小和标的目的的有向线段。
·向量没有位置,只要大小和标的目的。
·向量的箭头是向量的完毕,尾是向量的起头。
·向量描述的位移能被认为是与轴平行的位移序列。
 向量的暗示办法
向量的暗示办法
向量与标量:
1,向量有大小有标的目的,标量只要大小,没有标的目的。
向量与点的:
1,向量和点数学形式上相等,但几何意义完全差别。
2,点 有位置,没有现实的大小或标的目的。
3,向量 无位置,有现实的大小和标的目的。
4,联络 : 任何一个点都能够看做是从原点动身的向量。
零向量:
1,零向量是独一大小为零的向量
2,零向量是独一一个没有标的目的的量
3,零向量不是一个点,因为没有定义某个位置
4,零向量暗示的是没有位移,就像零标量暗示的是没有数量一样
标量与向量的计算
标量和向量之间不撑持加减法;
乘法 : 将每个重量都与标量相乘就能够
除法 : 等同于乘以标量的倒数
几何解释 : 向量乘以标量的效果是以标量的大小缩放向量的长度,负值则标的目的相反。
例 : -2(2,5) = (-4,10)
例 : (6,-2,-4)/2 = (3,-1,-2)
向量的模长
计算公式 :

几何解释 : 如图所示,当我们将所示向量做为斜边构建一个曲角三角形,所示向量的大小(模长)即可通过三角形狗固定翼推出。

尺度化向量 :
1,尺度化向量(单元向量)1,就是大小为1的向量。(适用范畴 : 仅需要晓得标的目的而不关心其大小。如 : 法线)
2,运算法例 : 将向量除以他的大小(模长)。

例 : 尺度化像含量(12,-5)
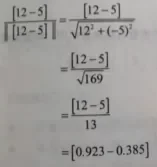
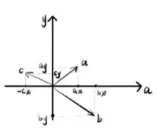
向量与向量的加减法计算
1,计算公式 :
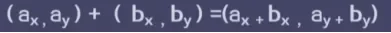
2,加法 : 对应位置相加 例 : (1,-4) + (7,5) = (8,1)
3,减法 : 对应位置相减 例 : (-3,6) - (-4,3) = (7,3)
4,几何解释 :

计算两点间间隔 : 间隔公式
1,计算公式 :

2,应用范畴 : 计算一个向量到另一个向量的间隔 (a 到 b 的位移向量为b - a)
3,几何解释 :

向量的点积计算
乘法之 ——点积(又称点乘,内积)
1,计算公式 :

向量点乘就是重量乘积的和,成果是一个标量并满 *** 换律 a1,·b = b·a
点积的几何意义与向量投影
几何解释 : 点乘成果描述了两个向量的“类似”水平,点乘成果越大,夹角角度越小,两个向量越接近。
a·b = |a||b|cosθ


投影的几何解释 :

兰伯特光照模子
兰伯特光照模子是目前最简单通用的模仿漫反射的光照模子。使光照标的目的的反标的目的为L向量,法线标的目的为N向量,则有:
L与N标的目的不异 则 Nor·Light = 1(纯白)
L与N标的目的相反 则 Nor·Light = -1(纯黑)
L与N标的目的垂曲 则Nor·Light = 0(纯黑)


向量的叉积计算
乘法之——叉积(又称叉乘,叉积)及运用于3D向量
1,计算公式 :
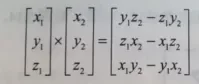
不满 *** 换律 : a x b != b x a
满足逆交换律 : a x b = -(b x a)
1,向量叉乘即便重量穿插相乘再相减,成果是个向量且不满 *** 换律。
2,几何解释 : 叉乘地道道的向量垂曲于本来的两个向量。
向量叉积的大小与标的目的判断
1,计算公式 : ||a x b || = ||a|| ||b|| sinθ

