高斯九岁便能快速算出1到100的总和,十一岁时便能导出二项定理的一般展开式,并对无限级数的展开颇为熟稔。那么,如许一位身世贫穷的神童,他是若何一步步成为“数学之王”的呢?他若何将本身的数学才气应用于天文学的计算傍边?在与本身同时代的数学家拉普拉斯、勒让德、贝瑟尔等人的交往中又发作过哪些故事?
撰文 ∣ 颜一清(辅仁大学数学系)
1850年代的高斯高斯(1777-1855),出生于德国Brünswick一穷困人家。 他从小就有算学异禀。他的才智遭到本地Brünswick[注1]公爵的存眷, 公爵就不断帮助他完成大学教育,获得博士学位,并出书数学巨著《整数论研考》(Disguisitiones Arithmeticae)[注2]。
高斯年冠十九,就在数学上有无以复加的表示:他打破数学史上两千多年的沉寂, 以曲尺与圆规做出正十七边形的图形来。并且他维持如斯出色的研究量量达半个世纪之久。 他的研究范畴普遍, 广泛纯数学与应用数学,研究内容新颖、深切。 那使他成为十九世纪科学范畴上最凸起的人物。 他在曲面学上的研究, 更是扶引黎曼缔造黎曼几何学,并诱发二十世纪初爱因斯坦做出广义相对论来。
高斯就业以后不断定居在哥廷根(Göttingen)。他逝世后不久,哥廷根处所的领主汉诺威王乔治五世(George V)[注3] 为表扬他的丰功伟业,敕令铸造一个七公分曲径的纪念章赠与高斯家族。纪念章边沿以拉丁文刻着“Georgius V. rex Hannoverage Mathematicorum principi”(汉诺威君主乔治五世向数学家之王致敬)[注4]。 从此, 称号高斯为“数学之王”的名号风行一时。
一 出身
Johann Friedrich Carl Gauss(洗礼名, 后来他常用 Carl Friedrich Gauss) 在1777年4月30日出生于 Brünswick 的一贫穷劳工人家。 他的父亲叫做Gebhard Dietrich Gauss(1744-1808),母亲是 Dorothea Benze(1743.6.18-1839.4.18)。
高斯的祖先姓 Goos,是德国北部 Völkenrode 村的新教徒人家。高斯的祖父 Jürgen Goos 是曾祖父 Heinrich Goos 三次婚姻中最初第二个儿子, 在家他没有什么份量,只能往外埠求开展。他成婚后于 1739 年到 Brünswick-Wolfenbüttel 公国的首都 Brünswick 定居, 改姓 Gauss。 起先因为没有置产, 在其时的同业工会的限造下,只能做零工糊口。好不容易贷款购得一所斗室子栖身了十四年,生育三男一女。后来换房子到 Wilhelm 街30号。1774年7月5日债未还清,他就因肺病逝世。他的老婆早他三个月故去。长子 Gebhard 一贯帮忙他父亲做工,就由他负责偿债。不外他也跟弟妹谈好,房子归他继承,弟妹分得一些现款(借来的)做为抵偿。那些债 Gebhard 费了二十五年才还清。
Gebhard 在1768年与 Dorothea Vernecke 成婚, 第二年1月14日生子Johann Georg Heinrich。1775年9月5日他的老婆因肺病逝世。1776年4月25日 Gebhard 与邻村的 Dorothea Bentze 再婚。1777年4月30日他们在 Wilhelm 街30号的家里生下数学天才高斯。高斯是 Dorothea 独一的孩子。Dorothea 在成婚前当过7年女佣。 她没有正式受过教育,不会书写,印刷体字勉强能够念。
Gebhard做过形形 *** 的工做,最初十五年他只处置造园业。因为他会书写,也管帐算,他当过一家葬仪社的管帐。
高斯曾经向他的再婚对象 Minna Waldeck 描述过他父母亲:“父亲是一位诚恳、忠厚的人,在外头他得他人的尊崇。但是在家里他是个暴君。好在我很早就不消依靠他,相互间的抵触较少。母亲个性顽强、明朗、仁慈又伶俐。在我与父亲有抵触的时候,她很包庇我。我很亲爱她。”
高斯的外祖父是位石工,因工做使然的空气污染,30岁便得痨病逝世了。高斯有一位舅父 Johann Friedrich,他自学成精巧的织缎人才。那位舅舅与高斯很亲,他常会讲一些话引起高斯的猎奇心 , 他觉得高斯好伶俐。 当他在1809年逝世时高斯叹伤:“一位生就的天才过去了。”从父母亲的祖先来看,他们都是一些农工阶级的人, 子孙能出高斯如许的神童可是个异数。
二 幼少年时代
有关高斯小时候的故事都是高斯晚年向跟随他的人们说的。他记性好极,并且反复论述中并没有收支的情形,所以他的话可信度大。
高斯很小的时候家门前有一条濠沟(后来围起来)曲通 Ocker 河。 春天一到, 濠沟里涨满了水。 有一次小高斯在沟边玩耍时掉进沟里, 在他溺毙前被路过的工人救起, 逃过一劫。
在炎天 Gebhard Gauss 是一家砖瓦工场的管工,到礼拜六得给工人们发薪。有一回他要发薪,3岁的小高斯站起来 :“爸爸, 算错了。”在世人目瞪口呆之下重算的成果证明小高斯是对的。
高斯7岁时进 St. Cathrine 小学。 教师是 J. B. Büttner。 班上有百来个学生。 教师在屋顶低、 地板凹凸不服的教室里拿着鞭子来回走动。 鞭子是教师教、惩两用的。高斯在如许的情况下安然无事过了两年。在高斯九岁摆布时,Büttner在算术课上要学生们“写出1到100的数字来, 并求出它们的总和”。 写好的同窗把运算用的石盘(其时纸张仍是豪侈品) 翻下放在教师桌子上。 再来交的同窗依次叠上石板。教师想,出如许的考题他能够平静一下了吧。 没想到高斯一会儿就把石盘拿去教师桌上放了,说:“我交了。(Brünswick 土语, Liggest se!, 英译:there it lies)”其他小伴侣汗流夹背地忙着运算。高斯默坐着, 不睬会教师奇异的眼神。成果大部门的小伴侣都错了,因而挨了打。高斯的石盘只见 5050 那个数字。他给教师的解释是:1 + 100 = 101, 2 + 99 = 101, … , 50 + 51 = 101。 所以 1 + 100 等于有50对101, 谜底即是 5050 。
那件事的发作有它象征性的意义。末其一生高斯做出来的成果都是简洁而准确的。 但是世人必要它有详尽的解释。
高斯的亲戚们听到到那件过后曲摇头。因为根据鄙谚, 神会让他宠受的人夭折,那孩子的寿命恐怕不长。
教师Büttner履历那件过后觉得他再也没有什么可教给高斯了。于是特意从汉堡为高斯买一些好的算学书如 Remer 著《Arithmetica》(在扉页上有高斯的签名及1786年12月6日字样), 或 Hemeling 的《小算术计算书》。 那两本书都有被频繁利用过的陈迹与许多小孩子计算的笔迹。
Büttner有一位助手 Martin Bartels(1769-1836)。他的工做是替小伴侣削鹅毛笔,矫正他们的书写等。他是白铅细工匠的儿子,住在高斯家附近。可能是 Büttner 或是 Bartels 跟高斯的父亲 Gobhord 筹议过高斯往后的教育问题。做父亲的认为高斯与异母兄 Georg 一样,未来走定他本身的路子:当工人。他哪有钱供儿子念书呢?对方可能找得到崇高人士出资给高斯读书。从此顽固的父亲在晚上不再要高斯织必然量的亚麻丝,以至把纺车带到后院劈成块,当柴烧了。取而代之的是 Bartels 与高斯常在一路挑灯夜读。他们交成好伴侣。Burtels 1788年后又去读书,专攻数学,后来成为 Kasan 大学的传授。
高斯在11时便能导出二项定理的一般展开式,并对无限级数的展开很熟稔。于是神童高斯的名字传遍 Brünswick。
在 1788年经由 Büttner 或 Bartels 说服不情愿的父亲,高斯末于进入 Brünswick 的预科学校 Katharineum。在那儿学生的年龄相若。高斯早些时的处所德语也矫正成官方德语了。数学教师 Helling 之一次看过高斯交的功课便批示,那么优良的学生用不着再来上他的课。高斯在阿谁期间又得到年长伴侣 Bartels 与 J. H. J. Meyerhoff(1770-1812) 的帮忙自学拉丁语与希腊语。 那些古代语言对念古典册本是必须的。
有一天高斯看书看迷了,走进 Brünswick 公爵的御花园而不自觉。却是公爵夫人看到了他,夫人讶异那么一个小孩莫非看得懂他拿着的书?一问之下才晓得实的看得懂。改天她叫仆人找高斯过来给公爵看。公爵发现那个内向、拘束的14岁小孩确实很伶俐。
Bartels在1788年进入 Brünswick 的 Caroline 高档学校,认识了那里的数学传授 E. A. W. Zimmermann(1743-1815)。Zimmermann还兼 Brünswick 公国参事,跟公爵情谊很深。Barters介绍高斯给Zimmermann。 后者便与 Brünswick公爵讨论高斯那个小孩。 末于在1791年公爵引见高斯, 并决定昔时6月起给高斯10个 thaler (德国旧银币) 的年金外加一些其他用费。 他还获得一些书本做奖赏,此中有一本是 Schulze 的《对数表》。高斯常常利用它, 还签上“Gauss, 1791”。
其时有风俗, 贵族或是有钱的商人会帮助家境贫苦人家的资优子弟读书, 以备未来他们用材之需。
高斯既然得到 Brünswick 公爵的年金念书, 做父亲的 Gobhard 再也没有理由反对他升学了。
1792年2月18日至1795年间高斯在 Caroline 高档学校进修。 那所学校在其时是德国更佳学府之一。 学校的学科新颖, 传授优良, 图书典藏丰硕。 它的教学设想除了因应生活的现实需要外还教育学生们成为新文化的梢公, 并出力培育学生们成为有自在思惟与崇高情操的人。 从德国的那一类学校, 十八、九世纪人材辈出。
跟高斯一样是贫民家的孩子而得到帮助进入那所学校的人其时有 Bartels、K. Ide(与高斯同业,早逝)、 Meyerhoff(修订高斯在《Disquisitiones Arithmeticae》中的拉丁文)等人。
高斯在 Caroline 高档学校期间读了许多古典文学名著, 因而他的文学素养很好。 他念的数学名著有欧拉、拉格朗日与牛顿等人的著书。 末其一生高斯对牛顿十分爱崇。 在著作方面他也进修牛顿的做风。[1]
那时候法国大革命(1789年)已然发作,但是在拿破仑挥兵攻打邻国以前,德国的一切情况还沉睡在十七世纪以来的半封建轨制里。[2]
很小高斯就喜欢做数字游戏。 他算得又快又好。 在1792-1793年间高斯做量数散布的研究。 他把整数以千为品级找出其间所含的量数个数。 根据亚历山大时代的埃拉托斯特尼(276-194 B.C.),整数 p 所含量数不大于 √p, 并由挑选法可求得量数个数。 而高斯则由察看得出量数个数的增加率 D(n)= π(n)− π(n − 1000)(π(n): 2至n间量数个数,n ≥ 1000)与
成反比。 因而由几何图形来看,
π(x),
。高斯也想过
的情形, 但认为后者的表达体例固然比力简单, 误差却比力大。高斯在那时候又得到另一本对数表, 是瑞士 Johann Lambert 写的。 再加上他本身的运算(他对对数熟稔得很)。 如许才获得上述的成果来。 往后他还常“对数中有诗情”呢!但他并没有颁发量数散布的成果。
1798年法国大数学家勒让德(Adrien-Marie Legendre,1752-1833) 颁发了较准确的量数散布公式:
,
。命运的做弄使得往后高斯与勒让德所发现的数学内容常呈现交织在一路的情形。
三大学时代
高斯并没有驯服 Brünswick 公爵的意思选读公爵领地的赫尔姆施泰特(Helmstedt)大学, 而筹算赴 Brünswick 约65里以南的哥廷根大学就读, 公爵仍是容许了。
哥廷根大学在 1737 年由英王兼汉诺威大公乔治二世(George II)兴办, 故那所大学又以英王的名字 George Augusta 称号。 它的形式模仿牛津大学与剑桥大学, 比其他德国大学有较好的情况与前提, 也比力不受 *** 与教会的干涉。高斯喜好那里的学术自在的风气与丰硕的馆藏, 所以选择去那儿念大学。
高斯在1795年10月5日注册, 成为哥廷根大学数学系学生, 那时候他拥丰年金158 thaler 与伙食费。 他对未来的出路感应徘徊。 语文与数学都是他喜欢的, 而学语文以后出路较好。
在大学之一年他借的书有25本。 此中20本是文科的书, 只要5本是数学书。
1796年3月30日是高斯生活生计中决定性的一天。从那一天起,他起头写那出名的科学日志。 他把他的发现依次记载到1814年7月9日[日志在 1898 年从高斯在德国独一 (也是独一他见过)的孙子Carl August在Hamlin的家中找出]。3月30日的日志用拉丁文写着:
“等分圆周的原理以及用几何办法十七等分圆分等等。
3月30日,Brünswick”
据说从那一天起头他决定处置数学的研究,而语文成为他末生喜欢进修的一个癖好。
高斯对发现正十七边形的几何做法的记载是:“在Brünswick家里的一个假日,我思虑
的诸根之间的算术关系。隔日早上还没有起床, 我已经很明晰地看到我需要的关系式。 我就立即把它应用在正17边形上。 计算的成果证明那个办法是对的。”
1796年6月1日的《一般学艺新闻》中有高斯的通告:
一般的几何初学者都晓得如何做出正多边形, 如等边三角形、正五边形、正十五边形或是把它们的边数加倍的正多边形。在欧几里得的时代各人就已经能够做到那些了。 而从那时候起各人认为初等几何学末行在那个地步。 至少我不晓得有人胜利地迈出阿谁界限。因而我的新发现有出格的意义。我发现不但是上述那些正多边形,还有更多的正多边形可用几何法(只利用曲尺与圆规) 做出。做正十七边形的办法只是一个包罗更多内容的定理的特例罢了。 我还没有完全证出那个发现,比及完成后我会公开它。——哥廷根大学数学研究学生 C. F. Gauss那是高斯一生中仅有的一次预告他的发现。 后来“等分圆周”呈现在高斯巨著《整数论研考》的第七章,正十七边形的顶点求法成为那一章的一个例子。那本书因经费与出书商的问题迟延到1801年9月29日才出书,一出书就被抢购一空,形成一时的颤动。
1809年1月6日高斯从哥廷根给他的学生兼伴侣 Gerling 信, 说研究“整数论研究”所带给他的喜悦是他研究数学傍边登峰造极的。 即便多美的天文学上的发现所带给他的喜乐都无法与它比拟。 信中他给 Gerling 简述正十七边形的求法:
高斯好满意做出正十七边形来。 他对大学时代的老友 Wolfgang von Bolyai (1775-1856) [注5] 说, 以后他的墓碑上就刻上正十七边形好了。(模拟阿基米德。阿基米德很中意他所求得的球体与其外切圆柱的体积与外表积及它们的比例 2: 3。 成果他的墓碑上就刻着一球及其外切圆柱。 多年后罗马雄辩家西塞罗做西西里长官时,在荒芜中凭那个墓碑找出阿基米德的坟墓,修复了它。)[5]。
Bolyai是匈牙利 Transylvania 处所的贵族, 晚高斯一年进哥廷根大学哲学部分。 他与高斯初度在天文学传授 Seyffer 家碰面。Bolyai 对根底数学有兴趣,便毫无顾忌地议论数学, 就如许引起高斯对他的兴趣。 再下一次巧遇时他们便结为好伴侣了。高斯工做累了,就去 Bolyai 居处休憩而往往不先发言, 以至于不讲话。只要一次他显得很高兴,那是他做出正十七边形的时候。他给 Bolyai 他算出正十七边形的条记当做纪念。他们也交换烟斗, 每天在必然时间抽烟斗来驰念对方(在高斯逝世后,Bolyai 将那些工具寄去哥廷根大学留存)[6]。
高斯也带 Bolyai 徒步到 Brünswick 造访高斯的双亲。当高斯退席时母亲 Dorotea 问 Bolyai 她儿子能否成器?当Bolyai告诉她“他是欧洲之一等的数学家呢!”时,Dorotea听得热泪盈眶。
1798年9月28日高斯学成(没有比及拿博士学位)回 Brünswick。行前他跟 Bolyai 相约一年后由 Bolyar 定出时间及地点再见一次面。他们约在1799年5月25日礼拜六在哥廷根与 Brünswick 半途的 Claustal 村碰头。两人徒步同时抵达那儿,一路攀登一座小山。在山麓上的小酒店两人含泪握手道别。他们通信到高斯逝世前两年,但不断没有时机再见到对方。Bolyai 是高斯大学时代沉思、欢乐与共的伴侣。 尔后高斯再也没有向其他伴侣那么坦诚告白他的心思了。
1840年 Bolyai 在他的回忆录中记述:“……我认识了高斯,他那时候是哥廷根大学的学生。我们不断都有友善的接触。我历来不跟他比拟。他很谦善,也不夸示。我们几年在一路,我都没有看出他的伟大。很可惜,我不懂得翻开那一本无言、无题的书原来翻。我不晓得他懂得几,他倒看清晰我,但高估了我,不认为我有多细微。我们分享对数学的热爱与对道德的信念。我们时常在一路漫步,各自浸淫在本身的思虑中,几个小时不扳谈一言。”
高斯在哥廷根大学固然念数学,可与天文学传授 Seyffer 熟悉, 事后也不断有手札往来。 他也喜好物理学家 Lichtenberg、语言学家 Heyne(非诗人 Heyne),但不喜好数学传授 W. Kästner。
四 《整数论研考》的问世
1998年9月底回到 Brünswick 后,高斯前途未卜。但他不再回父母亲家而租屋在 Wenden 街。他写信给 Bolyai,期盼公爵能在经济上继续撑持他到找到工做为行。他也找过工做,但都失去时机。
昔时10月他到赫尔姆施泰特大学, 利用那里的图书。馆长善待他,数学传授 J. F. Pfaff(1765-1825)也对他很友好。他在忙着完成《Disguisitiones Arithmeticae》(编注:整数论研考,也译做算术研究)那本书。11月时他已修订第五章四次,第七章根本上完成了,第八章还得花好多时间。12月中旬公爵容许继续给高斯年金158 thaler。 在那以前年金迟迟未发下,高斯以借贷过活。公爵没有立即许诺继续给高斯年金有他小我的理由:他的父亲挥霍过度,使国库枯槁,几近破产。公爵想了法子,才挽救了那个场面。
公爵要求高斯拿博士学位。高斯原来筹算交给赫尔姆施泰特大学《Disqusitiones Arithmeticae》做为博士论文,但是印刷情况迟缓,高斯写的份量又越来越多,印刷费可不雅,超出预算。 因而,高斯打住出书第八章的念头。在1799年4月高斯筹算另交博士论文, 选题为“代数学的根本定理”。5月他完成它交给 赫尔姆施泰特大学当局。那是高斯做的有关“代数学的根本定理”之一次证明。尔后他又用另一些体例给了它三次证明。
那时候他起头展示大学时代天文学传授 Seyffer 给他培育出来的兴趣:天文学。4月间他做出计算视差的公式来。他也研究算术几何均匀数(arithmetico-geometric mean)、双纽线(lemniscate)与三角函数间的关系。
1799年7月16日高斯在赫尔姆施泰特大学无面试获得博士学位。公爵替他付出一切所需费用。
1799年12月高斯住在 Pfaff 家继续做他的研究。Pfaff家人一天之间只能见到高斯两三个小时。Pfaff 为高斯的安康着想,会带他进来走走,谈聊天。
昔时12月23日高斯发现算术几何均匀数 M (a, b) 与之一阶椭圆函数有如下的关系 :
12月16日高斯给好伴侣 Bolyai 信告诉他现状,还要他切记元旦(到那一天信应该已经抵达) 半夜那18世纪的最初一刹那。 对高斯来说,它将是一个出格神圣的时刻:在那一瞬时,尘世会从他面前消逝不见,他的人会升华成纯净的灵魂,体味出莫大的生之喜悦。
1800年高斯的时间就花在《Disquisitiones Arithmeticaes》的完成,印刷与椭圆函数上。他住在赫尔姆施泰特到1800年的新生节。他末于决定不在《Disquisitiones Arithmeticaes》加第八章以节省印刷费。即便如许公爵还逃加费用才付得清一切开收。
他又继续做椭圆函数的研究,也颁发计算新生节日期的公式。据说高斯的母亲不记得高斯的生日,只晓得他在耶稣升天节前八天的礼拜三出生。高斯做出算式才推算出他的生日来。
1801年9月29日《Disquisitiones Arithmeticaes》末于出书了,费用全由公爵付出,书一会儿被卖光,里手激赏。
在书的序文中高斯把那本书呈现给Brünswick公爵,文辞中充满谢意。他写:“假使没有公爵您的撑持,我无法毫无悬念地处置生就心仪的数学研究达数年之久。没有您的雅量与支持,我就无法除去迟缓出书那本书所遭碰到的所有障碍……” 公爵的名字因那篇序文而永存。
《Disquisitiones Arithmeticaes》以拉丁文写成,而高斯为求文笔的流利还请他的伴侣,拉丁文专家 Meyerhoff 矫正。那本书被称为“有七个封印的书”,意即由七章所成的艰深、难读的书,连专家都不容易看懂。书中那简洁的综合性证明所蕴涵的宝藏经由他的后进狄利克雷(P. G. Lejeune Dirichlet,1805-1859) 及后来的克莱因(Felix Klein,1849-1925)[4]等人的解,世人才气得以分享。
那本书的前三章处置二项同余式理论。第四章展开同余式平方剩余的理论。第五章讨论二元二次形式,并开展成三元二次形式的理论。第六章讨论第五章的特殊情形,第七章被视为书中的精华。高斯利用二项同余式理论来解代数方程式 xn=1,n∈N。从而应用在n等分圆周及正n多边形的做图上。[7]
高斯晚年说:“《Disquisitiones Arithmeticaes》已经成为汗青性的著做了。”他的话是对的。
尔后高斯投入天文学、物理学等的研究,不断到晚年才全神回到数学的研究上来。
五 投入天文学的研究
1800年代在天文学上是停顿敏捷的一个期间。不雅测天文学在手艺与仪器上都有长足前进。而天象图是由有系统的不雅测材料编辑而成的。在理论天文学方面,天王星在1781年被发现(海王星在1846年,冥王星迟至1930年才被发现)。那对计算星座的扰动(Perturbation)的准确性很有帮忙。
1801年是高斯划时代的一年。事后他回想起来,觉得有那么多科学实理涌如今他脑海中,使他无法抵挡。
1801年元旦意大利天文学家 G. Piazzi(1746-1826)在巴勒莫发现一颗小彗星Ceres(谷神星),它不带尾巴,也没有外被(envelope)。不断到2月11日他才不雅测到 Ceres 的轨道9°, 事后它就在太阳暗影下不见了。 根据“波得法例”(Bodes law), 那个星应该存在,并在1801岁尾或1802岁首年月再呈现。于是欧洲的天文学家们忙着算出Ceres再呈现的轨道。 而他们所能按照的是Piazzi 颁发在德国的《天文月刊》9月号上的所有不雅测数据。
高斯在昔时的9月29日才出书《Disquisitiones Arithmeticaes》, 但是那个讯息立即引起他的兴趣。Piazzi固然前后不雅测了41天。可也只要三天的不雅测数值。 在高斯的日志第119、第120项(1801年9月与10月) 里,高斯记下他起头算 Ceres 的轨道。高斯想,肯定有一个椭圆轨道合适 Piazzi 给的数据。那问题即是:天空上有两个星,地球与 Ceres 在各以太阳为一焦点的 C1与C2二椭圆上运行(开普勒第必然律)。而地球的轨道C1已知,并有三条空间曲线(不雅测线) 发自C1至C2。 两曲线间的C2弧已知,要求出C2曲线。[8]
1801年11月高斯完全处理了那个问题,就跟浩瀚天文学家们一样,他把成果颁发在《天文月刊》上。德国 Seeberg 不雅测台长兼《天文月刊》编纂 F. X. G. von Zach(1754-1832)按照高斯颁发的轨道,在1801年12月31日至1802年1月1日看到 Ceres。1802年1月1日,不来梅的 H. W. M. Olbers (1758-1840) 也在高斯预测的轨道上看到 Ceres。由此天文学家们为 Ceres 的再现狂喜不已。同时高斯的名声传遍了全世界。各人认为他是之一流的理论天文学家。早先高斯在天文学界默默无名。他没有天文学家该具备的仪器,以至于连千里镜也没有。但是那位数学天才单凭三次数据就准确地算出消逝不见的彗星的轨道出来。
高斯在1802年1月18日写信给 Olbers 问他不雅测 Ceres 的成果。那是他们间友谊的起头。Olbers是一位胜利的开业医生兼出色的业余天文学家。他看病人到晚上十点,事后在家里屋顶上的不雅测站看天象。据说他每天的睡眠时间不超越四小时。其时德国的天文学家们很喜好围绕在 Olbers 的身边。他是他们的原动力,并且从他的不雅测站可能能够获得一些新的不雅测数据,若是他们凭那些数据有新发现,则能够名垂不朽呢。
1802年 Olbers 在 Ceres 近旁发现一新星叫 Pallas。1804年 Ludwig Harding发现一星叫 Juno。 那些星的轨道当然全权委托高斯来计算了。高斯一个小时能够算出一个彗星的轨道来,而欧拉用古老法例须花上整整三天时间。
1801年夏圣彼得保大学想礼聘Ziemann。Brünswick 公爵为了留住他,升任他为枢密参谋官,并让他辞卸 Catharine 高档学校的教职。那个缺原来高斯有望,但是后出处高斯先前的教师、博物学家 Hellwig 继任。公爵可也要留任高斯,就把他的年金升为400 thaler,酬庸他写出《Disquisitiones Arithmeticae》。高斯听到那个动静后不由叫出:“可是我都还没有为那个国度做任何事啊!”他便公费买了一个六分仪, 供给 Brünswick 的人们利用。
高斯被全世界公认为名人的事实是,给他的赠与纷至沓来。1802年1月31日他被聘用为圣彼得堡科学院外国通信会员。同年9月5日又有邀聘请高斯当圣彼得堡天文台长。高斯在犹疑中。Olbers 听到动静后为了要留住高斯在德国境内,他动用他的关系,想让高斯当将成立的哥廷根天文台的台长。而公爵的反响是,又增加了高斯的年金。高斯觉得如许很好,他没有固定官职,但能正式为公爵工做。如许的地位合适他的癖好与需要。
1803年6月2日高斯给 Bolyai 信,信中说天文学与地道数学是他心中的罗盘指针经常指向的两极。
六 成婚
高斯的母亲成婚前在鞣皮工厂主 Ritter 家帮佣。高斯出生后 Ritter 家两个男仆人当他的教父。 因而高斯小时候常常去 Ritter 家玩。 圣诞节时那里必然有一份 高斯的礼品。从哥廷根回来后,高斯有时机就往 Ritter 家走动。他享受那里的 Brünswick 中产阶级家庭中协调的气氛。在那里,高斯与 Johanna Osthoff(1780.5.8-1809.10.11) 认识了。 她是另一名鞣皮工厂主 Osthoff 家独一的孩子。她长得优美,脾气明朗、可亲又明事理,也受了一些教育。
1804年6月28日高斯给 Bolyai 信说,他认识了一位他巴望成为末身朋友的美妙女子近一年。她斑斓的面庞犹如圣母般,闪现身世心的安然平静。她个性活泼,快活并且谦虚。尤其重要的是,她有天使般的爱心。1804年7月2日高斯给Johanna求婚信。信中他说他的未来姑且不谈,目前他拥有的足够两个年轻人不劳累地快乐过日子,他所可以供给给她的是他那一颗温暖、充满着爱的心。
对高斯的信Johanna拖了三个月没有答复。高斯的名气太大,立场高不成攀等使她实在犹疑了一阵子。高斯不解Johanna的缄默。不外其时的政局起头让他分心,并且不安起来。那时候拿破仑已攻破德国南方诸邦,起头以他的体例朋分德国境内一些小国。高斯固然依附 Brünswick 公爵,拿年金过日子,但是未来的变数蛮多。
Johanna 末于容许了高斯的求婚,他们在1804年11月22日定亲了。
定亲后三天,高斯满怀喜悦地给 Bolyai 写信说,他三天前定亲了。 现在人生在他面前似乎是永久的春天般充满着荣耀。 他并劝 Bolyai 也做做实地天文学,它仅次于在那人世间他所能尝到的甜美,又充满喜悦的纯数学实理的研究。
1805年10月9日,高斯与Johanna在 St. Catarina教堂成婚,住在 Ritter 家所拥有的房子 Steinweg 22号。高斯独身时也住在那儿。
在Olbers那里高斯认识了贝瑟尔( Friedrich Willhelm Bessel,1784-1864)。其时贝瑟尔年方20,在不来梅一家贸易机构干事。 因为他喜好天文学,也就结识了Olbers。 后来贝瑟尔成为尝试与理论两边面都是之一流的天文学家。高斯固然跟 Olbers 有深交,但是往后对 Olbers下的冷峻评语是:“Olbers在天文学方面实在做了很大的奉献。 但是他更大的奉献在于适时发现了贝瑟尔在天文学上的才气, 而为科学栽培了他。”
Olbers介绍贝瑟尔给高斯为的是要贝瑟尔替高斯阐发不雅测数据。 他们初度碰头较晚,但高斯给贝瑟尔深入印象,高斯给贝瑟尔的《Disquisitiones Arithmeticae》那本书,贝瑟尔爱不舍手,磨损后又从头拆订。贝瑟尔末其一生认高斯为师。而高斯也给贝瑟尔更好的评价。 两人之间从此有42年(中间连续过一阵) 的手札往来。 那些内容是研究高斯最有科学价值的数据。
1806年8月21日高斯喜获一子。高斯为纪念 Ceres 发现者 Piazzi, 以 Piazzi 的名字Joseph定名长子。
高斯与家人在 Brünswick 安静地过日子, 但其时政局越来越不妙了。拿破仑在稳固他的地皮,而普鲁士与奥天时没有防卫法国的一致性观点,形势看来很邪恶。于是普鲁士留意到联盟国的俄罗斯,便在1806年1月30日派Brünswick公爵为特使往圣彼得堡参议结合攻防法国是宜,但没有获得成果。却是圣彼得堡许多人士问公爵有关高斯的事,并请他放人,让高斯承受他们的邀请。
当3月23日公爵一回国,为了要留住高斯便决定再升高斯的年金为 600 thaler, 高斯在他生日当天听到那个动静。在5月高斯找一天造访公爵,表达谢意。那是他们最初一次的碰头。前后十四年的交往中公爵给高斯很大的学术研究时机,接着的数月 *** 使公爵再也无暇顾及高斯了。
普鲁士为了要阻挠法国权力向中欧蔓延,在1806年10月策动战争,而以年迈七十的 Brünswick公爵(他是 Fredrick 大帝在七年战争中的名将) 为统帅。 战场由耶拿(Jena)战到奥尔施塔特(Auerstaedt)。在10月14日晨,公爵在发号指令时被敌方的毛瑟枪伤到。 弹丸由公爵的右眼上方射进,打碎鼻梁;从左眼窝挖出左眼来。受伤的公爵退出战场。有一小队代表团派往拿破仑军营陈情:希望拿破仑以军人的宽宏大量让 Brünswick 公爵能在家人围绕中咽气。 但是他们遭到情感低落的拿破仑的嘲弄与侮辱。为了制止成为阶下囚,濒死的公爵只要流亡一途。
那时候高斯住家在公爵邱邸的正对面。10月25日清晨高斯被忧郁的马车声惊醒。从窗口他看到长形的双头马车载着弥留的公爵像柩车般渐渐地驶往汉堡门。公爵末于在 Altona(汉堡附近的一都会) 处所的小旅舍逝世。从此,高斯恨透了让他的恩人遭遭到如斯下场的拿破仑与法国那个国度。
早先Brünswick公爵有意在 Brünswick 为高斯建造一座天文台,先大方解囊让 高斯购置一座十英尺长的千里镜。它迟迟才安设好,反射镜颠末批改研磨后效果好极。但是要成立天文台,谈何容易!
颠末Olbers的周旋, 在1805年高斯将是建造中的哥廷根天文台台长已成定局了。 但是1806 年10月的战争使原来从属汉诺威王国的哥廷根酿成为法国权力下的威斯特伐利亚(Westphalia)王国, 国王是拿破仑小弟Jerôme(他统治不到10年)。
1807年7月25日高斯正式收到哥廷根大学的礼聘。 成果 Collegium Carolium 当局因传授指使,来索求高斯利用的千里镜。高斯认为千里镜要归赫尔姆施泰特大学的 Pfaff 传授保有才气阐扬那一座千里镜的功用。但是他的定见没有被采用,那使他怏怏不乐。他就在不快中分开Brünswick。太太 Johnnna 对 Brünswick 各式不舍,因为她的亲友全在那儿。
七 哥廷根时代的起头
他们一家人在1807年11月21日抵达哥廷根。住进旧天文台边的一座老旧房舍。 那时候汉诺威旧政体已经崩溃,威斯特伐利亚新 *** 尚未构成,所以高斯制止了正式向 *** 做就任宣誓的为难排场。
高斯当哥廷根天文台长兼哥廷根大学传授都还没有领到薪水,法国就已经向新 *** 发令征收战争金,而高斯的份是2000法郎。那在其时是一大笔钱。有一天 Olbers 寄来 2000法郎给他。不久拉普拉斯来信,告诉高斯他已经在巴黎替高斯付清了那一笔钱。高斯退还了Olbers的钱,至于拉普拉斯,高斯后来加上利钱还清了那笔钱。高斯还收到了一笔从美因河畔法兰克福(Frankfurt am Main)寄来的1000 frolin(德国境的一种旧币)匿名捐款,那回他收下了。 事后他得悉那是法兰克福大公为佩服高斯的功绩,从公款挪出的钱。
科学家兼探险家洪堡(Alexander von Humbolt,1769-1859) 在1804年从南美航海之旅回到巴黎时听到法国科学界对高斯的一片赞扬声, 使他对高斯印象深入。 后来他在1807年与高斯认识,并多年努力于罗致高斯到柏林大学,但最末没有胜利。他与政治家哥哥威廉(Wilhelm von Humbolt,1767-1835) 比高斯更早在哥廷根大学学过。 三小我后来成为末生莫逆之交。
1808年2月29日高斯通知他的双亲当天 Johanna 生了一个女娃, 并以发现 Pallas 的 Olbers 的名字定名为 Wilhelmine。 各人称她 Minma。高斯可惜Minma要在四年中才有一个生日。 同年4月14日高斯的父亲逝世。
1808到1809年间,舒马赫(H. C. Schumacher,1780-1850)来哥廷根跟高斯学天文学。 他记下他与高斯的对话成书,叫做《Gaussiana》。 那本书对后世研究他们两人很有帮忙。他们的交往持续到舒马赫逝世。 两人的书简集共六册。
1809年9月10日高斯的次子 Louis 降生。 他的名字是为纪念 Juno 的发现者A. L. Harding,而以 Harding 的名字定名的。Harding从1807年起成为高斯在哥廷根天文台的副手。
生 Minna 时 Johanna 夫人已经是难产,那回生完 Louis 三十一天,在10月11日她便逝世了。高斯悲哀已极,写信给Olbers :“昨夜八点我盖上了我的天使的双眼,在那里,五年来我寻觅到我的天堂……” 确实他们的婚姻生活十分完竣。高斯给 Bolyai 的信中就有过描述:“我快乐地过着家居生活。当小女儿长出一颗牙齿或是小儿子学到一个新词儿,那在家里就像发现了一颗新星或是新的实理那般重要。”
Johanna的葬礼后高斯动身到不莱梅找 Olbers, 回程去 Altona 找舒马赫, 又去 Brünswick 找素交寻求安慰。1927年高斯的孙子Carl在祖父的书堆中找出高斯悲悼亡妻泪痕斑斑的信,信有两部分, 第二部分是在不莱梅写的,日期是10月25日。之一部分他诉说,原来认为亡妻是他永久的朋友,没想到她一会儿就走了。 她不断只以他的快乐为念, 并原谅他的错失。但望她的灵魂能永久陪伴他,给他力量,让他不用沉,好好顾问三个小孩子。第二部分的信中高斯写他很孤单。 围绕他的人们让他暂时忘却痛若,但事后悲痛却酿成双倍来袭击他。她最初的丁宁是教他不要被哀痛打倒。但望她的爱与仁慈能活生生地永留他的心中,能助他有勇气斗争下去。
高斯口中“心爱的小 Louis”却在1810年3月1日猝死,跟随妈妈,走了。
高斯的第二部巨著《在太阳四周回转成圆锥曲线的天体之运动论》(Theoria motus corporum coelestium in sectionibus onicis Solem ambientium)在1809年成书,由其时最出名的出书商 F. C. Pertes 印刷。原来他用德文写,后来遵从 Pertes 的定见,为普及起见写成拉丁文。 内容是高斯根据开普勒的法例,做出圆锥曲线(椭圆与双曲线;物线不适用) 运动之下的天体轨道计算办法的完全系统。并从不雅测天体的三个点决定恒星或彗星轨道的一般办法。书的内容末于最小二乘法的讲解。
那本书以形式上简洁,文笔文雅、有完美性及首创性著称。其时常有新星呈现,天文学家们不能不借它来计算星座的轨道, 因而出书后有四十年之久它成为天文学家们必需精通的教科书。所以学者们对《运动论》的评价很高,世界各地的学会也就争聘高斯为他们的会员了。 法国科学院更在1810年赠送他 Lalande 奖 [为纪念法国数学家及天文学家 J. J. LeFranc ̧ais de Lalande(1732-1807) 所设立的奖] , 高斯拒受。 后来科学院秘书与 Sophie Germain(1776-1831) 动用奖金的一部门买一座天文摆钟送他,他那才承受,还末生安排那一座钟在他的房间里。
Sophie Germain是法国女数学家,她生在巴黎富有人家,自修数学。她为免受岐视, 以 Le Blanc 的男性化名寄出论文,遭到拉格朗日( Lagrange,1736-1813)赏识而出名。 她也以Le Blanc 为名在1804岁尾与高斯通信讨论《Disquisitiones Arithmeticae》,给高斯深入的印象。当1807年3月法军入侵 Brünswick 时,她怕高斯遭到危险,请法国军官去问候高斯。到此, 她才掀开她的女子身份。 她的次要奉献在于整数论。 她也因弹性外表的数学理论获得法国科学院的大奖(Grand Prix)。1837年哥廷根大学百年庆时高斯可惜她已逝世, 不然她的成就足够哥廷根大学赠与她荣誉博士学位。
高斯其实不重视最小二乘法(Least squares), 他认为许多处置数值计算的人天然会利用到它。 他在1794年就晓得它。1798年在机率计算顶用上它,1802年天文学的运算中也用到它。但是勒让德在1806年正式颁发了最小二乘法的理论(名称是勒让德定名的)。勒让德 *** 高斯在1809年的《运动论》中提及最小二乘法,不外事实上高斯早在1795年(应该是1794年)就创造了它。 后来拉普拉斯当他们两人的仲裁员, 裁定勒让德在颁发上有优先权,但两人都别离创造了最小二乘法。勒让德必定在其他他辛苦研究出来的功效上又跟高斯的创造反复, 如数论中平方剩余的彼此法例、超越函数以及几何学的根底理论等。
高斯的研究情感也有低落的时候。 在1807到1810年间,他写的有关椭圆函数的条记中突然呈现一句用细铅笔写的字:“过如许的日子不如死掉的好。”
八 再婚
为了要获得心灵上的安好以处置研究工做, 并让孩子们能得到妥帖的赐顾帮衬,高斯很快就想到再婚。他选择的对象是 Johanna 夫人在哥廷根的好伴侣 Minna Waldeck(1788.4.15-1831.9.12)。她是高斯在哥廷根大学的同事,法学传授 Johann Peter Waldeck 的小女儿。 她其时刚刚解除与他人的婚约,正心灰意冷的时候。高斯先得 Minna 双亲的首肯后写信给Minna。 他坦陈在太太逝世不到半年就向她求婚必然不会给人好印象。确实,亡妻的影子不断无法从他心中消逝,现在他也只能献出半颗心来。不外历来亡妻很亲爱 Minna,坚信 Minna 很愿意替代亡妻顾问高斯和孩子们。但望 Minna 能为她本身熟虑后再做决定。Minna容许了亲事。他们在1810年8月10日成婚。高斯那么快便再婚实在让亲友老友大吃一惊。那回高斯邀请他母亲从Brünswick过来同住。但是 Minna 是贵族身世,他的母亲犹疑到1817年才容许下来。
Minna料理家庭,也很敬服前人留下来的两个孩子。那使高斯对 Minna 满怀感谢与谢意。那一次的婚姻也算完竣。Minna并给高斯生了两男一女:Eugene(1811年7月11日生,三男), Wilmhelm(1813年10月23日生, 四男) 与 Therese(1816年6月9日生,次女)。
哥廷根天文台的建筑不断迟延下来。 曲到1810年威斯特伐利亚 *** 为天文台的建造工做做了五年方案, 筹算投入20万法郎来完成它。
威斯特伐利亚 *** 并给高斯贵族封号 Ritter von Gauss, 来酬劳他学术上的奉献。那一年柏林大学邀约高斯去教学,但他与 Minna 成婚已加深了与哥廷根大学的关系,并没有容许那个邀请。
1811年8月,天空上突然呈现一颗闪亮的大彗星。高斯在8月22日黄昏时分看到它。几天后他起头不雅测,那时 von Zach 八月初旬的不雅测成果已经到手了。 由那些高斯算出那颗大彗星的物线轨道。 它再现时公然在高斯算出的轨道上, 并印证他的预言,亮度加强了。 而欧洲的人们则视那颗大彗星为一代霸主拿破仑起头落败的预兆。
1812年1月30日高斯在哥廷根皇家科学学会上颁发超几何级数 1+
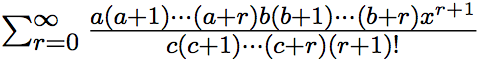
的论文。那个级数因a,b,c 取出格的数而可成为二项级数、对数、三角函数等解析学上很重要的级数。高斯是首位对无限级数的收敛性做出研究的数学家。
1812年6月底拿破仑率领近45万大军攻打俄罗斯而取道德国。之前拉普拉斯向拿破仑进言请他对哥廷根大学出格照顾。 因为那儿住着现代最顶尖的数学家高斯。
那回的战争拿破仑吃了瘪。俄罗斯军既不迎战,也不讲和却不断撤退,并利用坚壁清野战术。而俄罗斯冰凉的冬天也到了,法国军又冷又饿,末于在10月19日起头撤离。但一路上俄罗斯军与德国等联盟军结合起来逃击,法国军落败得很惨, 回到法国的残兵只剩下9万余人。
由拿破仑撑腰的威斯特伐利亚王国跟着拿破仑的退位(1814年4月6日)在1814 年崩溃。哥廷根又归属于汉诺威王国。
尔后十年是高斯功效丰盛的期间。 他出了二十数篇范畴普遍的论文, 此中有理论及不雅测天文学、曲面论、整数论及对数的问题等,还给代数根本定理另两种证明。
1816年9月17日哥廷根新天文 *** 成了。高斯一家人搬进天文台边西翼的宿舍。
九 处置地形丈量的工做
早在1816年6月8日舒马赫给高斯一信,说丹麦王出资让他丈量丹麦境内(昔时的丹麦疆土包罗一部分现今德国领土)的经纬线。他问高斯有没有兴趣。高斯在7月5日的信中答复, 若是是在汉诺威境他很愿意参与丈量工做,也愿意协助三角座(次要的三个地点) 的计算问题。于是舒马赫运用他的关系,末于在1818年9月由诺威辅弼正式委任高斯做 Luneburg 处所(事后又扩大范畴)的丈量工做。(汉诺威地域靠近荷兰边沿的在拿破仑时代已丈量过)

高斯不单是名义上的丈量队(也有戎行参与)主持人,他还实地参与丈量工做。那是费时又费精神的工做。高斯起先没有想到一投入那个工做竟持续了十年之久。 那期间炎天他几乎是在外埠过的。他怕热,气候燠热的时候他很难受。1822年他那当炮兵预备军官的长子 Joseph 也参与丈量工做,并且做得很好。
1826年后,高斯固然不参与实地丈量工做。但是丈量数据的整理消耗好多时间:得到野外的丈量数据后高斯单独投入与丈量有关的计算到1848年。那才做成汉诺威王国全域三角化丈量3000个据点的坐标。那些成为描画汉诺威王国地图的根本材料。
1823年贝瑟尔看不惯高斯为丈量工感化掉他的精神和时间,写信给他 :“那些工做次等的数学家就能够完成,用不着您去做。”高斯回他的信说,确实集世界上所有丈量功效也不值一个学问前进的定律。但是有时候我们得以相对性来判断价值。他也不克不及够从那现实上有用的工程抽身。 一则他能够做得比他人好, 二则他不做,那个丈量工做便流产了。 还有一件事请贝瑟尔保密:自从1810年威斯特伐利亚 Jêrome 王给他订薪后他的薪水不断没有调整过。为了维持他那一各人子的生活, 他愿意得到那一份工做所带给他的报答。
1824年10月底回到家高斯才发现整个炎天家里参差不齐。三个孩子得了麻疹,后来又传给已经病了两年的 Minna 夫人,使得她一时盘桓在存亡之间。
亚历山大·冯·洪堡在其时德国的细密科学开展上饰演了很重要的角色。他在普鲁士宫廷上很有影响力,又很识才。他想把鲁普士所属柏林大学(1810年设立)酿成像巴黎的工技学院(Ecole Polytechnique)那般超卓的学校。 因而他一而再再而三地鼓动高斯去那儿当校长,不消教书,尽管研究机构就得。汉诺威 *** 听到那个动静后赶紧通知在伦敦的英王。不久国王批示高斯的年薪调升为2400 thaler。那也跟 *** 赏识他的丈量业绩有关。高斯于是消除了去柏林大学的意愿。
1821年在野外工做中高斯创造了回光仪(helitope)。它是配有一个能扭转的镜子的光学仪器,镜子可使光线朝向一个固定标的目的反射,而不受远方的玻璃或亮光物等反射的干扰。在三角化工做时回光仪能够当发光的目的物,也能够做为光的通信。因为从四、五英里外看它有一二级星的亮度。
在三角化空中的现实工做中对曲面有了领会,高斯于是在1827年颁发了有关曲面的论文。他把曲面以参数式暗示,并讨论曲面自己具有的性量(intrinsic property),如高斯曲率K 在保长变更下稳定等性量。
后来高斯的学生黎曼( Berhard Riemann,1826-1866)把高斯的曲面理论发扬光大, 成为黎曼几何学。爱因斯坦就利用黎曼几何学才创造了广义相对论。
十 与韦伯合做
1828年高斯赴柏林参与学术会议住洪堡家,在那里他认识了其时当 Halle 大学讲师的威廉·韦伯( Wilhelm Weber,1804-1890) 。洪堡鼓舞高斯做地磁气的研究。 那一年高斯升任哥廷根大学正传授。
1831年因高斯的保举,韦伯被聘为哥廷根大学物理学传授。昔时高斯54岁,韦伯27岁。尔后除了1843-1849年间待在莱比锡外,韦伯不断在哥廷根。高斯与韦伯起头合做。 起先韦伯只是高斯纯熟的辅佐,后来韦伯的独立性与重要性日增,他更高的成就在于1846年的电力学测定。
1832年高斯写了有关磁气测定绝对单元的论文。 在那里,数学家高斯又成为“测定物理学”的立法者了。
高斯与韦伯合做,创造了电磁式电信机 。 他们在天文台与物理研究所之间安装接送机互通信息。1834年他们在天文台附近建造了一所磁气不雅测所。 他们在 1840年共著《地磁气地图》(莱比锡出书),奠基了位势论的根底。
到此高斯在应用数学的研究抵达了他生活生计中的顶点。 但是他成就的核心与基盘仍是在他投入了青春的纯数学上。 他专注的范畴是算学、代数与解析学。
十一 孩子们
高斯的大女儿 Wilhelmine(昵称 Minna)长大后边幅神似她母亲,个性却像高斯。 她是高斯最钟爱的孩子。 她顾问祖母、生病的继母和弟妹,并与出外工做的父亲通信。
1830年9月15日Minna与哥廷根大学神学与东方语言传授 Heinrich August von Ewald(1803-1875)成婚。Ewald年轻时就已经是出色的学者,人品好,但十分心不在焉。高斯对他那位女婿很满意。Minna婚后不久罹患肺病,没生孩子。 不外Minna与Ewald过了很幸福的婚姻生活。
高斯的第三子Eugene在数学与语文方面承袭了父亲的才能,但是他背叛性强,性格又暴燥。 原来Eugene上大学时驰念语言学,做父亲的却用他的权势巨子硬压造下来。Eugene“听劝”念法令系。但是他进校后猛赌牌、酗酒,所欠的债当然由老子了偿。在高斯怒斥之下Eugene不带一物,不告而别。高斯托舒马赫在Eugeine可能去的汉堡寻找。 末于在不来梅找到Eugene。高斯带行李与钱赶到不来梅Olbers 家。在那里父子生别了。1830年12月 Eugene 买棹赴纽约。他的行径伤透了病中的 Minna 夫人的心。她自从生完三个孩子后常常生病,还带些忧郁症,又很在乎高斯对她的不雅感。孩子们的事也让她不顺遂。Eugene难惹, 她的第二子 Willhelm 比力温顺,喜好务农,但去过几处练习,都不克不及适应。后来总算在波茨坦做了两年生意。
长病的 Minna 夫人在1831年9月12日逝世了, 遗言Eugene的行为改好才气得到他份内的遗产。Minna夫人过世并没有打倒高斯。 他羽毛已丰,有学术与社会地位,孩子们也已长成。家事改由小女儿 Therese 主持。母亲 Dorothea 还健在,使高斯比力内省,会回想到他的过去,也就常对访客谈及他的儿时。但是他的人变得弧僻。他心中不快活,觉得没有什么好再斗争的了,看待一些年轻同业也就冷峻起来。 为了贝瑟尔没有来信吊问 Minna 夫人的亡故,高斯生气与贝瑟尔隔绝通信。 多年后他们又恢复写信,但是相互间已经有一层隔膜了。
两个儿子Eugene与Wilhelm的问题使高斯没辙,常常与他的学生兼伴侣C.L. Gerling筹议。 总算在1837年 Wilhelm娶了贝瑟尔的侄女,并在同年与新娘子移民美国,以实现他运营农场的梦。小舅子也同业。那回Wilhelm夫妇得到了高斯的祝愿,不外他们的行程也让高斯担忧了好几个月。
十二 非欧几何学
有关欧几里得的平行公设(parallel postulate)早在纪元二世纪托勒密(Claudius Ptolemy,ca. 85-ca. 165)就置疑了。 他想把它从公设中挪开而没有胜利。事后历代都有一些人测验考试那个问题。曲到十九世纪那个问题的研究成为一种时髦。高斯与他的伴侣Bolyai就透过那个问题的讨论加深了相互间的友谊。高斯也不断断断续续地研究平行公设。在1799年9月的日志中他写:“在几何学的原理上我得到了很好的停顿。” 在1846年10月2日高斯给 Gerling 的信中说:“在没有平行公设的几何学上,多边形的面积与其外角和减去360°成反比。它应该是那个理论上的之一个定理,也是起点。我早在1794年就得到那个理论。”
Wolfgang Bolyai 自1799年归去故土特兰西瓦尼亚(Transylvania)到1804年他当上 Maros Vásárhely 的数学与物理传授之前把数学弃捐了一阵子。事后他又持续他昔时做的平行公设研究。1804年9月16日他把所得成果寄给高斯。11月25日高斯给他回信,赞扬 Bolyai 所下的时间, Bolyai 得到的成果有些与高斯的类似,但是它并没有完全处理了问题。高斯又说,他筹算有生之年打破那个问题的难关,不外目前他忙其他事,无法灌输在它上面。若是 Bolyai 可以克制障碍处理问题,高斯很愿意让给好伴侣优先发现者的荣誉,并设法让世人晓得。
Bolyai 遭到那封信的鼓舞,1808年12月27日又寄补遗给高斯,但是没有收到回音。他们之间的通信就连续到1816年。
1816年 Bolyai又写信给高斯说:想把儿子Janus 送到哥廷根高斯那里,先当学徒后念书。但也没有得到回函。那期间Bolyai又在平行公设上投入了好多精神而无成果。
Walfgang Bolyai 的儿子Janus小时候从他父亲受教育,他进修敏捷,十三岁时父亲生病他都能够代课了。他又继承了他父亲对第五公设的狂热,他几乎被平行公设迷住了!1818年Janus在念维也纳的陆军手艺学院,并在1820年写信告诉父亲他在测验考试平行公设的研究。做父亲的得知后大吃一惊,去信劝儿子:“连一个时刻都不要用在那个问题上,它不克不及给你任何成果,反而会迫害你整小我生。它会褫夺你的闲暇、你的安康、你的歇息、你生射中的一切幸福。 那个暗黑的无底深渊可能会吞噬万万个牛顿般的人物,它不成能在那个空中上见到光。”
可是Janus没有听进父亲的忠告,反而愈加勤奋去研究。1823年11月3日他起头觉得到成功的滋味,他告诉父亲:“从‘无’中我缔造出新世界来。”他所得成果即是高斯在持久的疑惑与犹疑后在1816年达成的。高斯在1816年的书评中颁发说,证明平行公设是不成能的事。他为那遭遭到严苛的攻讦。因而他决定在他有生之年不再颁发有关平行公设的任何定见。
不久高斯发现一名法令学家 F. C. Schweicart(1780-1859) 在1812-1816年间不借助于第五公设开发“天界几何学”,他给高斯他的“天界大小的理论”的简稿,收罗高斯的定见。高斯答复:他写的全数似乎是借高斯的笔写成的一样。高斯又说,空间存在于我们的外部。它的原则不克不及预先记述。它的性量该用尝试为根底才气完全确定。
Schweicart 有外甥 F.A.Taurinus(1794-1874),他也是一名法令学家,因舅父的书给他 *** ,他从年轻时就投入平行公设的研究。1824年10月Taurinus寄给高斯他的尝试式的证明。 同年11月8日高斯给他长信。请他保密信的内容。信中说:“三角形内角和小于180°的假设会引导我们到出格的几何学,它里面不会有矛盾产生。我开发那种几何学到很满意的水平,除了一破例我全数能够处理有关它的问题。那个破例即是定命的决定,而它是不克不及预见的。那个定命获得越大,越接近于欧氏几何学,取无限大值则两者一致……” (注:那个定命便定为
,K:高斯曲率)Taurius遭到鼓励,1825年写出《并行线的理论》, 1826年写《几何学的次要要件》寄给高斯。 两书序文中都提到高斯。高斯不再理会他,那些书也就默默无闻了。
1825年Janus起头写他的论文。 他的父亲告诉他:“若是你实的胜利地处理了有关平行公设的问题,有两个理由你得赶紧颁发它。一则,不雅念很容易传开,他人可能也会颁发它。 二则,如预言会同时在数处呈现,春天里紫罗兰会四处开花一般, 许多事会同时发作,所以你要抢先公开它。”
Janus的《绝对几何学》以附录的形式呈现在他父亲写的教科书《Tentamen》中(“Appendix scientiam spatii absolute veram exhibens” 1831年6月出书)。
1831年 Walfgang Bolyai 把书与信别离寄给高斯。高斯收到了信,书因霍乱的蔓延无法寄达而被折回。高斯在1832年2月从伴侣处拿到了那本书。
1832年3月6日高斯给 Walfgang 信说:Janus 的成果与高斯的成果十分一致,令他很惊讶。 不外他未便称赞 Janus, 因为那么做等于称赞他本身。 他向年轻的几何学家 Janus 暗示非常的佩服之意,并给他一个问题:若何求出非欧几何学里面一个四面体的体积? (后来两人都做出那个问题)
Walfgang关于高斯的回信内容相本地满意。但是Janus却十分绝望并愤怒不服:高斯不给他公开的认定,还说在创造上他有优先权!
其实俄国数学家罗巴切夫斯基(Nikolai Ivanovich Lobachevsky,1793-1856)早在1829-1830年间在 Kasan 大学学报 Kasan Messenger 颁发他的《虚数几何学》(非欧几何学)了。罗巴切夫斯基在1815-1816年间起头在 Kasan 大学教几何学时还试图证明平行公设。后来他逐步习惯于不成能证出平行公设的事实,从而开展出无平行公设存在的几何学,并把研究成果在Kasan科学学会(1826年2月12日)上提出。 不断到1830年它才被刊载出来。
但是罗巴切夫斯基的论文并没有引起西欧人士瞩目,他于是在1837年用法文把他的《虚数几何学》的摘要颁发在Crelle Journal XVII(pp.295-320)上。1835-1838年间他又写出有关的研究论文。
Janus Bolyai 得知罗巴切夫斯基也做出非欧几何学后认为那是高斯搞出来的一种把戏,愈加生气,又泄气,就不再研究他的“斑斓新世界”了。从此他跟父亲Walfgang也疏远起来,还参军职退下,过他的荒唐生活至死 ,最初以至于连他本身的肖像都用佩剑刺破,悉数毁掉[11]。
高斯不断到1840年才晓得罗巴切夫斯基做出非欧几何学来,为了要好好念原文,高斯还特意重学了俄文,并在1842年选聘罗巴切夫斯基为哥廷根皇家科学会通信员。
十三 费马最初的定理
法国科学院曾经在1816-1818年间赏格收罗费马大定理 xn+ yn= zn,n ∈ N 的证明或反证明。Olbers写信给高斯,鼓动他做那个问题。高斯答复说,他感谢 Olbers 告诉他件事,不外他对它不感兴趣。事实上他也很容易做出连续串那一类孤立而没有应用价值,且使人难解的问题来。但是他认为那对往后数论的开展并没有多大好处。
现实上高斯证过 x3+ y3+ z3= 0 无整数解,即费马最初的定理当n=3的情形。 他在另一篇文章上也证过那个定理当n = 5的情形,但是没有再做下去。
十四 椭圆函数

从那些看得出高斯对椭圆函数是做过深切研究的。高斯可能有意把椭圆函数的全数理论完好地做出后再颁发,不然不公开它。高斯所写有关椭圆积分的内容只要在他1818年颁发的论文“Secular Perturbations”中能够见到。
多年后(1827年)挪威人尼尔斯·亨利克·阿贝尔(Niels Henrick Abel,1802-1829)与德国人雅可比( C. G. J. Jacobi,1804-1851)因高斯的《Disquisitiones Arithemetica》第七章335节中的提醒而做出关于椭圆函数的友善的合作性研究。对那高斯的立场是不理不睬的。
在1824年昔时22岁的阿贝尔解出一般五次方程式的不成解性,而在奥斯陆自印成六页的小论文。他把论文寄给列国数学先辈们,满怀希望得到他们一些好心的回应。 他也寄给高斯。但是他所得到的可靠动静是,高斯尖叫:“那里又呈现怪物了!”就把阿贝尔的论文扔去一边。(参看《张寿武:数学中的无解之解》)
1825年8月底阿贝尔因他的一篇论文(后来遗失)得到挪威 *** 的奖金可往西欧游学一年。阿贝尔的更大愿望是造访他爱崇的高斯。 但是高斯那小我既然高不可攀,阿贝尔便在9月取道丹麦,抱着痛苦的表情绕过高斯所在地哥廷根,抵达柏林。在那里他幸运地碰到A. L. Crelle(1780-1855)。Crelle是之一位在德国境内铺设铁路而发家的土木匠程师。 他喜好数学,并有识别天才的洞察力。阿贝尔、斯坦纳(J.Steiner,1796-1867)、魏尔斯特拉斯(Karl Weierstrass,1815-1897)都因他识才替他们颁发论文才得以出名。
Crelle 想办一份数学杂志,就向阿贝尔邀稿。阿贝尔便在1826年Crelle出资的数学季刊杂志Jaurnal für die reineund angewandte Mathematick(又简称Crelle Journal(I))上颁发了五篇论文。 该杂志第二册中有阿贝尔的椭圆函数双周期理论。
阿贝尔到了巴黎,那里的数学家们对他冷冷的,只是有礼貌罢了 。 他寄给巴黎科学院的有关超越函数的巨著也被审稿者柯西( A. L. Cauchy,1789-1857)放置在家里失踪了。 那篇文章不断到阿贝尔贫病交迫灭亡后几年,经挪威 *** 的 *** 才寻找出来,末于在1841年见到天日 (法国科学院论文集第7卷pp.176-264)。
1827年秋天阿贝尔在Crelle Journal上颁发椭圆函数的论文。 数月后 (1828年3月30日)高斯给贝瑟尔信,说:“我无法完成自从1798年以来研究的椭圆函数,因为我有其他事得做。比来我发现阿贝尔已经完成了我的工做,他让我省去三分之一的劳力。他写得既文雅又清晰。写的体例又跟我神似到令我诧异的地步。 不外他并没有剽窃我的研究,因为我历来没有跟任何人谈到它。”
1829年4月6日阿贝尔逝世了,年方27岁。同年5月29日高斯给舒马赫信, 说:“阿贝尔的死对科学界是一大丧失。我在报纸上都没有看到有关他的报导。若是你手中有那位特殊人物的生前数据,请告诉我。假使可能,我也想拥有他的肖像。”
如许看来,高斯对阿贝尔的印象并没阿贝尔所想象的那么差。
至于另一位椭圆函数发现者雅可比,在1849年庆祝高斯得博士学位五十周年纪念宴会上,他是哥廷根大学的高朋, 被摆设坐在高斯的旁边。雅可比想跟高斯谈数学,但高斯避开话题不谈。
十五 解聘七传授事务
英王兼汉诺威王威廉四世(William IV)在1837年6月逝世。 他固然不干练,倒也是一位慈祥的国王。 因为他无子嗣,英王由他的侄女维多利亚继承。她是女子,按照汉诺威律法不克不及继任汉诺威王位,改由她的叔父,威廉四世昏庸的五弟 Ernst August 当汉诺威王,称为乔治五世(George V)。
1837年9月12日至20日哥廷根大学庆贺大学成立百年庆。乔治五世与亚历山大·冯·洪堡都来参与。 庆典的排场浩大,热闹十分。 但是好景不长。
1837年11月乔治五世废行了前王威廉四世所订的民主宪法。于是哥廷根大学的七位传授 Dahlmann、G. G. Gervinus、W.E.Albrecht、Ewald(高斯女婿)、韦伯与格林兄弟(格林童话做者)联署 *** 书。 国王一怒,12月12日解聘那七名传授。有一阵戎行还开进,控造着整个哥廷根。
有人攻讦高斯,说若是他参加 *** 行列,则重量足,工作不致于如斯。可是高斯甘愿洁身自好,恬静过他的研究生活。他也怕闹事会影响到哥廷根大学的声誉。确实,哥廷根大学因那事受损,要恢复它的名声花了五十多年。
高斯过后未便为女婿Ewald说项,却是为韦伯驰驱过。 他托洪堡给乔治五世进言。在一次宴会上乔治五世跟洪堡说:“用我的钱,我能够召来芭蕾舞娘、娼妓、传授,要多有几!”洪堡一听便知趣,没提起替韦伯缓颊的事。而被解聘的七名传授们却是被其他大学争相延聘。
1838年5月Ewald受聘于图宾根大学为东方语言传授,高斯溺爱的大女儿Minna于是跟丈夫Ewald赴图宾根。Ewald在那里认实工做了十年。 而 Minna因肺病在1840年8月12日在本地逝世,让高斯十分哀痛。
十六高斯的教学晚年高斯对教学比力负责。 有一些优良的学生在他底下受教,在数学方面有爱森斯坦(F. G. M. Eisenstein,1844)、黎曼(1846)、戴得金(Richard Dedekind,1850)与数学史家 Moriz Cantor(1850)等。
1844年放暑假时爱森斯坦(1823-1852)带着洪堡的介绍信来见高斯。高斯看待爱森斯坦就好像爱森斯坦是他钟爱的儿子般,并期许爱森斯坦未来的数学成就可与阿基米德、牛顿并列。爱森斯坦在他急促的一生中留下了五十篇文章。 却是高斯认为爱森斯坦该有的地位被高斯自己代替了。
戴得金(1831-1916)描画过高斯上课的情形:“师生们围着一张方桌坐着。高斯不让学生记条记,要他们专心听讲。高斯很自由,清晰而平板地讲课。当他要强调某件事时他会以他那清亮的蓝眼睛盯着靠近他坐着的学生讲。 要写数学公式时他会站起来在他背后的黑板上用他那斑斓的字体不占处所地写下来。若是得认真推算的例子,他会带来写着不异数据的小字条来。”
十七 晚年
在高斯最初十数年,他看来仿佛完全安放在他那中产阶级的生活中。 他的母亲在1839年4月18日逝世,安享天算至97岁高龄。他在1840年出书《Atlas of TerrestrialMagneti *** 》。1843年4月6日出书《Memoir in Geodesy (I) 》 1846年又出书《Memoir in Geodesy (II) 》。1849年6月26日高斯早年的天文学家伴侣 Bernhard August von Lindenau(1799-1854)来造访他,让他好快乐。
1845岁首年月哥廷根大学的学术参议会委托高斯从头组合接近破产的传授寡妇基金会。高斯以他一贯的认实立场研究寡妇基金,处理了问题,挽救了那个基金会,使一批孤儿寡妇们很感谢他。
事实上高斯自己很会理财,他年薪有一阵只要1000 thaler。 他的收入是薪水再加上选课学生的膏火 (他的学生一贯很少)。 但是他生活俭朴,又因很会投资,他逝世后遗产竟有十五万三千 thaler,而从桌子、抽屉、衣橱又找出一万八千余thaler的现款出来[12]。
1848年2月哥廷根大学闹 *** 。激进派的学生领袖是Johann Miquel,他是 卡尔·马克思(Karl Marx)的好伴侣,有社会主义倾向。大都的学生是暖和派,他们仅主张校内变革罢了。戎行一度也开进哥廷根来。而学生与差人间稍有抵触,不外工作没有闹大。哥廷根大学因此次 *** 反而嬴得在汉诺威王国次于 Hildesheim,最前卫的学校的名声。
在此次 *** 中,学校当局请出体能好的传授们站岗,维持学校境内的次序。
Max Schneidewin 在1927年时回忆说 ,在1848年他6岁, 是哥廷根大学古代语言传授的儿子。2月事务时他看到他的父亲穿上黑外衣,配上宽厚皮带,荷蛇矛去Gei *** ar门边站岗。站岗的传授们听到住在附近的高斯要颠末,便排成列。当高斯颠末时他们便向他行举枪礼暗示敬意。
可见在同事们心目中高斯高尚的地位。高斯本人也意识到他君临学术界的架势。
现实上高斯也获得各类荣誉, 列国学术机构争聘他为荣誉会员, 他又有许多封号,如早在1810年8月19日威斯特伐利亚国王Jêrome 就封他为爵士 (Knight) ,1818年乔治三世(George III)赐封他参议 (Hofrat)。1845年乔治五世封他为首席参议 (Geheimes Hofrat)。 不外1848年4月20日高斯给 Wolfgarg Bolyai 的信中却说那些荣誉对他来讲比如是过眼烟云罢了。
1848年的2月事务后汉诺威 *** 为了要填补1837年事务以来的遗憾,想聘回被流放的七位传授,但也只要韦伯与 Ewald 回来哥廷根大学。那可是晚年的高斯十分乐见的事哩。
1848年哥廷根大学内设立了“文艺博物馆”,后来改称为“联谊会”, 高斯也是会员之一。 设立它的意图在于拉近师生之间的间隔,以免发作学生变革运动。 “联谊会”的地点设在一位希腊已故传授的宿舍。室内放置着各类非反动性的报章、杂志。 晚年的高斯漫步到那儿,从早上十一点到下战书一点,看报章杂志是他独一的消遣。高斯会把他要看的有关政治、经济、文学和科学的报章杂志以想看的挨次叠成一堆放在椅子上,再坐上去以免被他人拿走,再一份一份抽出来看,需要时做做札记。 若是有学生拿走他要看的报纸,他会盯着学生看,看得阿谁学生从容不迫站起来, 赶忙递给他那份报纸。 那么一来学生们便奉送他一个绰号:“报纸山君”(Zeitung-tiger)了。
高斯从年轻时代不断对语文连结高度兴趣。 他对德国文学与哲学很在行,而最喜欢笔名为 Jean Paul 的 Friedrich Richter(1763-1825)的做品 。 因为 Richter的人品像他的老友 Bolyai。 他读遍与他同时代的歌德(Goethe,1749-1832)的做品,可是不喜好,也不赏识另一做家席勒(Schiller,1759-1805)。法国文学他念蒙田与卢梭等人的做品。俄文学则他偏心普希金(1799- 1837)。 对英国文学他不喜好莎士比亚,觉得莎士比亚写的做品悲情太多。依高斯的话,“人世间悲剧已经够多了。”他很喜欢沃尔特·斯各特(Sir Walter Scott,1771-1832)的做品。 不外高斯会在鸡蛋里挑骨头。 他看到斯各特写“满月从西北方升起”大笑不已,立即矫正过来,还跑遍各书店查看那一句是不是印错了。
舒马赫与 Lindenau 在1850年、1854年相继过世,高斯常通信的老伴侣只剩下Gerling、洪堡与Bolyai。
1854年黎曼因高斯保举,要任职哥廷根大学的讲师,高斯从黎曼提出的三个标题问题中挑选黎曼匆促中加上的第三个:“On the Hypothesis that Underlie the Foundation of Geometry(英译)”。黎曼的演讲高斯听后赞赏不已。不外高斯最初的科学活动是跟Gerling讨论傅科钟摆的批改问题。 看来现实又详细的问题对他来说比黎曼的笼统复杂的概念问题要随便多了。
1854年高斯做过全身查抄,他的心脏有肥大现象,看来他的日子不多了。 但是他的安康又一时恢复过来,事后他还去听6月10日黎曼的讲师演讲会,也去参与哥廷根与汉诺威市间的铁路开幕仪式。8月后他脚肿,勉强只能在屋内走动。12月7日原来认为高斯已经不可了, 但是他又好转过来。
同年12月19日高斯的同事、心理学及动物学传授 Rudolf Wager(1805-1864)造访高斯。此君对宗教及灵魂等问题很有研究兴趣。23日与数日后 Wagner又来看高斯。高斯的家人及伴侣们很反对Wagner那个行为。Wagner也就没有公开他所做的条记,不断到 Wagner 逝世后才由他的遗物中找出一些记载。由此中能够看出高斯相信生命的永久。他说:“若是没有永久,人世是无稽的,而整个缔造是荒唐的。”
高斯不断拖到1855年2月23日清晨在睡眠中安祥逝世,享年77岁。 他带的怀表在去世几秒后停下,指针停在1点零5分。高斯的伴侣们坐在邻室陪同他,让他走完人生的那最初时刻。
1855年2月26日晨在哥廷根大学天文台不雅测所前的广场上举行高斯的葬礼。高斯的头上戴着桂冠,穿戴紫色大学礼袍,躺在黑色灵榇内 ,周遭环绕着初春的花朵。世人敬仰后灵榇由十二名专攻数学与科学的学生(此中包罗戴得金) 抬到天文台前的广场。 面临着浩瀚参与者,高斯的女婿Ewald与高斯的好伴侣,哥廷根大学的传授Sartorius von Waltershausen(之一位写高斯列传)致吊辞, 推高尚斯为无比奇特的天才,成就卓绝。葬礼后高斯被葬在哥廷根的St. Albans墓园。
高斯的脑被取下,它净重有410克,比拜伦(63.8 ounces)的轻,而比但丁(50.2 ounces)的重。高斯的脑有许多璇纹,纹路很深。
十八 后代
高斯的小女儿 Therese 自从姐姐 Minna 在 1838年搬离哥廷根后职掌家事,赐顾帮衬老祖母(1849年逝世)与高斯。 她素性忧郁,又多病痛。 在高斯逝世后一年的1856年9月23日,Therese与已通信十四年的演员兼剧院导演 Wilhelm Staufenau(1809-1886)成婚, 1864年2月11日逝世。Therese 没有孩子。
高斯在德国的子孙由 Jeseph 单传。 子孙中男丁在二次大战中或失踪或战死,只要一人生还。1936年后姓高斯的人只要三人,此中一人有心理碍障。高斯三男 Eugene 对他父亲不断有背叛情结。 他几乎销毁所有高斯给他的信。 以至于他分得的父亲遗物,一面乔治五世颁给高斯的金章,也熔化成金边眼镜框来利用。Eugene 与四男 Wilhelm 丁壮后在美国做生意胜利,酿成财主。他们的后代兴隆。
十九 结语
高斯遗留下来的文件及与他私家相关的信函,还有他出书过的书全由哥廷根大学搜集,并经哥廷根皇家科学院礼聘专家学者如菲利克斯·克莱因等十人从1863年至1935年才整理安妥成十二卷书出书。
高斯的座右铭是“稀少,但成熟” (Pauca sedmatura,Fewbutripe)。 他又主张做品不该该留下钻凿过的陈迹,就好像一座盖好的教堂毫不留下先前鹰架林立,辛勤奋做过的迹象般。所以高斯不多写,但写成的做品则以论述简洁、内容丰实著称。
正文
[注1] 其时的德国尚未同一,德国境内由三十九个有 *** 的小王国、小公国等所构成。
[注2]《Disquisitiones Arithmeticae》那一本书的七章内容历来没有被超越过,没有被弥补过,也没有被发现有任何的错误。高斯逝世后《Disquisitiones Arithmeticae》的第八章 (处置高次同余式)被找出来。 它是高斯早年因考虑出书经费太庞大而被割爱的。 在收录 《高斯全集》时它被放在之一册中, 成为《Disquisitiones Arithmeticae》的第八章,等于成全了高斯早年的意愿。
[注3] 英国在1688-1689年的名誉革命时英王 James II 及他信奉上帝教的儿子被逐出国外。1701年英国国会决议王位继承人须为新教徒。英伦三岛(英格兰、苏格兰及爱尔兰)同一于1707年。其时的国王是 Anne 女王 (James II 次女,信奉新教。在位1702-1714)。她的独子在10岁时夭折。她逝世后由 James I 外曾孙,新教徒 Hanover 选侯 George I(在位1714-1727)继承英国王位。他是一位只会讲德语的英王,为英国 Hanover 王朝之始。他的王位由长子 George II(在位 1727-2760) 继任。再来是 George II 的长孙 George III(在位1760- 1820)继位。George III 有浩瀚儿女。他的王位由长子 George IV(在位1820-1830)继承。他的独女早逝,王位便由 George III 三 子 William IV(在位1830-1837) 继位。那些英国 Hanover 王朝诸王兼而是 Hanover 选侯或王 (Hanover 在1814年才成为王国)。William IV 的独女早逝,英国王位便落在 George III 的第四子 Edward 的女儿 Vcctoria(在位 1837-1901) 身上。但是 Hanover 王国不认可女继承人,故由 George III 第五子继位,为George V。从此英王不再兼 Hanover 王了。又,Victoria 为英国 Hanover 王朝最初一人。
[注4] 英译为“George V,The King of Hanover,to the Prince of Mathematicians”。按“Prince”有小邦国之“王”的意思,其时的德国联邦由三十九个邦国所构成。
[注5] 德语国度人名中有“von”与法国人名中有“de”一般来说都是贵族姓氏。 那些字皆有“from”或“of”的意思 ,接着的姓往往是那小我的属地名称。
参考材料
[1] A. Guy Waldo Dunnington, “Carl Friedrich Gauss, Titan of Science” , Hafner Publishing Co. N. Y. 1955.
[2] W. K. Bühler,“Gauss,a Biographical Study” Springer-Verlag,N. Y. 1981.
[3] 高木贞治, 《近世数学史谈》,东京共立社,昭和8年 (1933)。
[4] Felix Klein, “Famous Problems in Elementary Geometry”,Translated into Enghish by Bemanand Smith,Boston,1897.
[5] Howard Eves, “An introduct ion to the History of Mathematics”,6th edition,Holt,Rinehart and Winston,N. Y. ,1990.
[6] Guy Waldo Dunnington, “Carl Friedrich Gauss”, Lousiana State University Press,Baton Rougge,1937.
[7] E. T. Bell,“Men of Mathematics”,Simonand Schuster,N.Y.1937.[8] Felix Klein, “Development of Mathematics in The 19th Century”Translated into English by M. Ackerman,Math. Sci. Press,1979.
[9] 数学 Seminar, 《100人の数学者》,日本评论社,东京, 1989。
[10] Tord Hall “Carl Friedrich Gauss, a Biography”, Transleted into English by Albert Froderberg,The MIT Press,Boston,1970.
[11] 数学 Seminar, 《100人の数学者》,日本评论社,东京, 1989。
[12] Tord Hall “Carl Friedrich Gauss, a Biography”, Transleted into English by Albert Froderberg,The MIT Press,Boston,1970.
本文原载台湾中央研究院数学研究所发行的《数学传布》杂志,《返朴》经受权转载。
