若是你晓得杨-米尔斯理论是啥,你就不会问那个问题了~
在上一篇文章《深度:宇称不守恒到底说了啥?杨振宁和李政道的发现事实有多大意义?》里,长尾君用了很长的篇幅跟各人聊了聊宇称不守恒的事。各人也晓得杨振宁和李政道先生因而斩获了全球华人的之一个诺贝尔奖,然而,对杨振宁存眷多一点的人就会经常听到如许一个说法,说宇称不守恒固然为杨振宁博得了物理学界登峰造极的诺贝尔奖,但那并非他的更高成就,杨先生更大的奉献是杨-米尔斯理论。
那下子良多人就懵圈了。杨-米尔斯理论是啥?上学的时候教师必定没讲过,去百度上搜,搜出来成果更是一头雾水,那都是只要懂的人才气看得懂的工具。模模糊糊能觉得到杨振宁先生仿佛做了什么十分了不得的工做,但是要详细说他做了啥,在科学上有啥意义,就含混了。
那杨-米尔斯理论到底重不重要?重要,当然重要,绝对的重要,那是现代标准场论和粒子物理尺度模子的根底。在讲宇称不守恒的时候我就说过,杨-米尔斯理论是一个布景愈加宏大的故事。宇称不守恒固然也影响了物理学的方方面面,但是我们把它零丁拎出来仍是敷衍了事能讲清晰的,而杨-米尔斯理论就纷歧样了,想要把它搞清晰,我们得把视角上升到整个物理学开展的高度上来,因为那是一个跟物理学主线亲近相关的故事。
01物理学的主线物理学家到底在研究什么?
大天然中有各类各样的现象,有跟物体运动相关的,有跟声音、光、热相关的,有跟闪电、磁铁相关的,也有跟放射性相关的等等。物理学家们就去研究各类现象背后的规律,然后他们得到了一堆关于运动啊,声学、光学、热学之类的定律,然后物理学家们就满意了么?
当然不满意,为啥?定律太多了!
你想想,若是每一种天然现象都用一种专门的定律来描述它,那得有几“各自为政”的定律啊。于是物理学家们就想:我能不克不及用更少的定律来描述更多的现象呢?有没有可能有两种现象外表上看起来毫不相关,但是在更深条理上却能够用统一种理论去描述?有没有可能最末用一套理论来描述所有的已知的工作?
那个工作,素质上就跟秦始皇要同一六国一样,我决不允许还有其他六个各自为政的国度存在,必需让所有人遵守同样的法令,从命统一个政令,用同样的语言和文字,如许才协调。物理学家的同一之路,也是如许汹涌澎湃地起头的。
牛顿同一了天上和地上的力,麦克斯韦同一了电、磁、光。到了19世纪,跟着人们对微不雅世界研究的深切,许多在宏不雅优势牛马不相及的工具,在微不雅层面上却很好的同一了起来。好比我们熟悉的撑持力、弹力、摩擦力之类的工具,在宏不雅上它们确实是差别的工具,但是到了微不雅一看:那些杂七杂八的力全都是分子间感化力形成的,而分子间感化力素质上就是电磁力。而且,那些分子、原子运动的快慢,在宏不雅层面上竟然表现为温度,然后热现象就酿成了一种力学现象。
于是,到了19世纪末,人类所有已知现象背后的力就都归结为引力和电磁力,此中引力由牛顿的万有引力定律描述,电磁力由麦克斯韦方程组描述。但为难的是,麦克斯韦方程组和牛顿力学那套框架竟然是矛盾的,那么到底是麦克斯韦方程组有问题仍是牛顿力学的那套框架有问题呢?
爱因斯坦说麦克斯韦方程组没弊端,牛顿的框架有问题。于是爱因斯坦晋级了一下牛顿的那套框架,在新框架下继续跟麦克斯韦方程组愉快的玩耍,那套晋级后的新框架就叫狭义相对论。
在狭义相对论那个新框架里,麦克斯韦方程组不消做任何修改就能间接入驻,那是一等公民。别的,牛顿力学里有些工具无法间接搬过来,但是略微修改一下就能够很愉快的搬到那个新框架里来,好比动量守恒定律(间接用牛顿力学里动量的定义,在狭义相对论里动量是不守恒的,需要修改一下就守恒了),那是二等公民。还有一类工具,无论怎么改都无法让它适应那个新框架,那是刁民。
刁民让人很头痛啊,不外还好,固然有刁民,但是刁民的数量不多,就一个:引力。牛顿的万有引力定律在牛顿力学阿谁框架里玩得很愉快,但是它骨头很硬,不管怎么改,它就是宁死不平狭义相对论那个新框架,那要怎么办呢?当然,我们能够继续改,我们相信固然如今引力它不平,但是以后总能找到让它服气的改法。但是爱因斯坦另辟门路,他说引力那小子不平改我就不改了,然后他别的提出了一套新理论来描述引力,相当于零丁给引力盖了一栋别墅。成果那套新引力理论极其胜利,并且爱因斯坦提出那套新理论的体例跟以往的物理学家们提出新理论的体例完全纷歧样,那种新手法带来梦幻般的胜利惊呆了全世界的物理学家,然后爱因斯坦就被捧上天了,那套新理论就叫广义相对论。
爱因斯坦用广义相对论征服了引力,用狭义相对论安设好了电磁力之后,接下来的路就很明显了:同一引力和电磁力,就像昔时麦克斯韦同一电、磁、光那样,究竟结果用一套理论解释所以的物理现象是物理学家们的末极梦想。但是,爱因斯坦穷尽他的后半生都没能同一引力和电磁力。不只如斯,跟着尝试仪器的前进,人们撬开了原子核,在原子核内部又发现了两种新的力:强力和弱力。
那下可好,不单没能同一引力和电磁力,竟然又冒出来两种新的力。所以,我们如今的场面酿成了有四种力:引力、电磁力、强力和弱力。此中,引力用广义相对论描述,电磁力用麦克斯韦方程组(量子化之后用量子电动力学QED)描述,强力和弱力都还不晓得怎么描述,同一就更别谈了。
到了那里,我们那篇文章的配角杨-米尔斯理论末于要退场了,我先把结论告诉各人:如今强力就是用杨-米尔斯理论描述的,弱力和电磁力如今已经实现了完全的同一,同一之后的电弱力也是用杨-尔斯理论描述的。也就是说,在四种根本力里,除了引力,其它三种力都是用杨-米尔斯理论描述的,所以你说杨-米尔斯理论有多重要?
同时,我们也要晓得,杨-米尔斯理论是一套十分根底的理论,它供给了一个十分精妙的模子,但是理论自己其实不会告诉你强力和电弱力详细该如何如何。盖尔曼他们把杨-米尔斯理论用在强力身上,连系强力各类详细的情况,最初得到的量子色动力学(QCD)才是完好描述强力的理论。格拉肖、温伯格和萨拉姆等人用来同一弱力和电磁力的弱电同一理论跟杨-米尔斯理论之间也是那种关系。他们之间的详细关系我们后面再说,那里先领会那些。
以上就是一部极简的物理学同一史,只要站在如许的高度,我们才气对杨-米尔斯理论有个比力明晰的定位。同一是物理学的主线,是无数物理学家们孜孜以求的目的,杨-米尔斯能在那条主线里占有一席之地,其重要性不问可知。有了如许的认知,我们才气继续我们下面的故事。
在物理学的同一史里,有一小我的工做至关重要,那个重要倒不是说他提出了多重要的理论(固然他的理论也极其重要),而是他倒置了物理学的研究体例。以他为分水岭,物理学家摸索世界的体例发作了底子的改动。恰是那种改动,让20世纪的物理学家们可以游刃有余的处置比之前复杂得多得多的物理世界,让他们可以斗胆的预言各类以前想都不敢想的工具。那种思惟也极其深入的影响了杨振宁先生,杨振宁先生反过来又把那种思惟发扬光大,最初产生了精妙绝伦的杨-米尔斯理论。
那么那小我是谁呢?没错,他就是爱因斯坦。那么,爱因斯坦究发现了什么,以致于倒置了物理学的研究体例呢?
02被倒置的物理学各人先想一想,爱因斯坦之前的物理学家是怎么做研究的?
他们去做各类尝试,去丈量各类数据,然后去研究那些数据里的规律,最初用一组数学公式来“解释”那些数据,若是解释得十分好,他们就认为得到了描述那种现象的物理定律,然后顺带着发现了隐藏在理论里的某些性量,好比某种对称性。在那里我们能明晰的看到尝试-理论-对称性如许一条线,那也契合我们凡是的理解。
但是,爱因斯坦把那个过程给倒置了,他发现上面的过程在处置比力简单的问题的时候还行,但是当问题变得比力复杂,当尝试不再能供给足够多的数据的时候,根据上面的体例处置问题几乎是一种灾难。
好比,牛顿发现万有引力定律的时候,开普勒从第谷不雅测的海量天文数据里归纳出了行星运动的三大定律,然后牛顿从那里面渐渐猜出了引力和间隔的平方反比关系,那个还敷衍了事能够猜出来。我们再来看看牛顿引力理论的晋级版-广义相对论的情况:
上图是广义相对论的引力场方程,你告诉我那种复杂的方程要如何从尝试数据里去凑出公式来?况且,广义相对论在我们日常生活里跟牛顿引力的成果几乎一样,第谷不雅测了那么多天文数据能够闪开普勒和牛顿去猜公式,但是在20世纪初有啥数据让你去猜广义相对论?水星近日点进动问题是少少数不契合牛顿引力理论的,但是人们面临那种问题,遍及之一反响是在水星里面还有一颗尚未发现的小行星,而不是用了几百年的牛顿引力有问题。退一万步说,就算你其时认为那是因为牛顿引力不敷切确形成的,但是就如许一个数据,你怎么可能从中归纳出广义相对论的场方程?
颠末连续串的深度碰鼻之后,爱因斯坦意识到当理论变得复杂的时候,试图从尝试去归纳出理论的体例是行欠亨的,洛伦兹不就是被迈克尔逊-莫雷尝试牵着鼻子走,最末才错失发现狭义相对论的么?尝试不成靠,那么爱因斯坦就要找愈加可靠的工具,那个愈加可靠的工具就是对称性!
于是爱因斯坦在物理学的研究体例上来了一场哥白尼式的革命:他先通过察看阐发找到一个非常可靠的对称性,然后要求新的理论具有那种对称性,从而间接从数学上推导出它的方程,再用尝试数据来验证他的理论能否准确。在那里,本来的尝试-理论-对称性酿成了对称性-理论-尝试,对称性从本来理论的副产物酿成了决定理论的核心,尝试则从本来的归纳理论的根底酿成了验证理论的东西。理解那一改变十分的重要,后面的物理学家都是那么干的,我们要先把思绪调对,否则到时候就容易呈现各类不适应。
爱因斯坦操纵如许思绪,先确定了广义坐标稳定性,然后从那个对称性动身得到了一套新的引力理论,那就是广义相对论。那也是为什么其他科学家看到广义相对论之后一脸懵逼,并且说若是不是爱因斯坦,恐怕50年之内都不会有人发现那套理论的原因。爱因斯坦是之一个那么反过来干的,广义相对论大获胜利之后人们才发现本来理论研究还能够那么干,那种思惟后来被杨振宁先生发扬光大,并构成了“对称决定彼此感化”如许的共识。
爱因斯坦完成广义相对论之后,继续朝着更伟大的目的“同一场论(同一引力和电磁力)”进军,在强力和弱力还没有被发现的年代,可以同一引力和电磁力的理论似乎就是末极理论了。我们如今都晓得爱因斯坦末其后半生都未能完成同一场论,但是同一场论的庞大光环和爱因斯坦自带的超等偶像的磁场仍是吸引了一些物理学家,也带来了一些有意思的新设法。
03标准稳定性我们再来理一理爱因斯坦的思绪:爱因斯坦把对称性放在愈加根底的位置,然后从对称性导出新的理论。他从洛伦兹稳定性导出了狭义相对论,从广义坐标稳定性导出了广义相对论,如今我们试图同一引力和电磁力,那么,有一个问题就会很天然地被提上日程:事实什么样的一种对称性会导出电磁理论呢?
那个问题很天然吧,但是它的谜底却不是那么好找的,那么容易就让你找到招致电磁理论的稳定性,天主岂不是太没体面了?麦克斯韦方程组是畴前人的尝试经历定律总结出来的,并没有指定什么详细的对称性,那要怎么办呢?
不焦急,诺特定理告诉我们对称性跟守恒定律是逐个对应的,我如今不是要找导出电磁理论的对称性么?那么我就去看看电磁理论里有什么守恒定律呗,更好仍是电磁理论里特有的。
说到电磁理论里特有的守恒定律,那必定就是电荷守恒啊。电荷必定是只要电磁学才有的工具,并且电荷守恒定律又是那么明显,不论是不是它,它必定是嫌疑更大的阿谁,必需抓起来严刑拷问,看看跟它私通的对称性到底是什么。
在外尔的严刑逼供下,电荷守恒招了:跟电荷守恒相对应的对称性是波函数的相位稳定性,(在量子力学里粒子的形态是用波函数来描述的,既然波那必定就有相位),但是因为汗青原因,那个相位稳定性我们不断称为标准稳定性,也叫标准对称性。
那个相位稳定性,或者说标准稳定性,我们怎么理解呢?为什么麦克斯韦的电磁理论里会有标准稳定性呢?若是从公式里看就十分的简单,就是我给它那里做了一个相位变更,它另一个处所就产生了一个相反的相位,总体上刚好给抵消了;若是从曲觉上去觉得,你能够想想,在量子力学里,波函数的模的平方代表在那里发现该粒子的概率,你一个波函数的相位不管怎么变,它的模的平方是不会变的啊。若是你还想继续深挖,我保举你去看一看格里菲斯的《粒子物理导论》(回复“粒子物理导论”能够获取那本书的电子版),他在第十章里专门用了一章来讨论标准理论,并且很通俗。
总的来说就是:标准稳定性招致电荷守恒。
但是工作还没完,外尔接着发现了一件实正让人吃惊的事:我们上面说标准稳定性招致电荷守恒,那里说的标准稳定性指的是整体标准稳定性,但是外尔发现若是我们要求那个标准稳定性是局域的,那么我们就不能不包罗电磁场。
泡利针对那个做了进一步的研究,1941年,泡利颁发了一篇论文,他在论文里严酷的证了然:U(1)群整体标准对称性对应电荷守恒,它的局域标准对称性产生电磁理论,以至能够间接从它推导出麦克斯韦方程组。U(1)群是群论里的一种群的名字,叫酉群(unitary group),或者幺正群,数字1暗示那是1阶酉群,我们如今只需要晓得对称性在数学上就是用群论来描述,并且凡是差别的理论对应差别的群(那里电磁理论就对应U(1)群)就行了。
也就是说,我们如今末于找到了决定电磁理论的对称性,它就是U(1)群的局域标准对称性。U(1)群和标准对称我前面都解释了,那么问题的关键就落在对称性的整体和局域的区别上了。
04整体对称和局域对称整体对称,望文生义,若是一个物体所有的部门都根据一个步伐变更,那么那种变更就是整体的。打个例如,舞台上所有的演员都同步地向前、向后走,或者全都做同样的动做,不雅寡看着演员都整整齐齐的,觉得所有人都像是一小我的复成品一样,如许的变更就是整体的。若是颠末如许一种整体的变更之后,它还能连结某种稳定性,我们就说它具有整体对称性。
有了整体对称的概念,局域对称就好理解了,类比一下,若是一个物体差别的部门根据差别的步伐变更,那么那种变更就是局域的。仍是以舞台为例,导演为了使演出更具有个性,他想让演员表示出海浪的样子,或者是千手不雅音那样,再或者是构成各类不竭变革的图案,那种时候每小我的动做变更就纷歧样了吧,也不会说所有人都像一小我的复成品一样了,那时候那种变更就是局域的。因为它不再是所有的人根据一个规则变更,而是部分的每小我都有他局域特有的变更规则。同样的,若是颠末如许一种局域的变更之后,它还能连结某种稳定性,我们就说它具有局域对称性。
从上面的情况我们看出来,整体变更要简单一些,所有的处所都根据同样的规则变更,而局域变更就复杂多了,差别的处所根据差别的规则变更。所以,很明显,若是你要求一套理论具有某种局域对称,那比要求它具有整体对称复杂得多,局域变更对物理定律形式的要求就愈加严酷一些。但是,你一旦让它满足局域对称了,它能给你的回报也会多得多。
仍是电磁理论的例子:整体标准对称性下我们只能得到电荷守恒,但是一旦要求它具有局域标准对称性,整个电磁理论,以至麦克斯韦方程组都间接得到了。电荷守恒和麦克斯韦方程组,那就是整体对称和局域对称给的差别回报,孰轻孰重不同很明显吧?电荷守恒是能够间接从麦克斯韦方程组里推导出来的。
以上是偏科普的解释,从数学的角度来说,整体变更就是你所有的变更跟时空坐标无关,局域变更就是你的变更是一个跟时空坐标相关的函数。跟时空坐标相关的函数,其实就是说差别的时空点,那个函数值是纷歧样的,也就是说变更纷歧样。
不管从哪种解释(从数学更容易),我们其实都能够看出:整体变更其实只是局域变更的一种特例。局域变更里变的是一个跟时空坐标相关的函数,但是那个函数的值也能够是一个定值啊,那时候局域变更就退化成整体变更了。
那么,一个斗胆的设法就产生了:在电磁理论里,整体标准对称性对应着电荷守恒,但是我一旦要求那个整体标准对称性在局域下也成立,我立马就得到了整个电磁理论。那么我可不成以把那种思惟推广到其他范畴呢?好比强力、弱力,有没有可能同样要求某种整体对称性在局域成立,然后能够间接产生强力、弱力的相关理论呢?
那是一个非常诱人的设法,杨振宁从他读研究生的时候就在起头揣摩那个事,但是不断到十几年后的1954年,也就是他32岁的时候才有成果,那个成果就是大名鼎鼎的非阿贝尔标准场论,也叫杨-米尔斯理论。
05杨振宁的“档次”在我们正式讲杨-米尔斯理论之前,我们先来聊一聊杨振宁先生的档次。
有一个曾经跟爱因斯坦共事过的物理学家如许回忆:我记得最清晰的是,当我提出一个自认为有事理的设想时,爱因斯坦其实不与我狡辩,而只是说:“啊,多丑!”。只要他觉得一个方程是丑的,他就对之完全失去了兴趣,而且不克不及理解为什么还会有人愿意在上面花那么多时间。他坚信,美是摸索理论物理中重要成果的一个指点原则。
爱因斯坦本身也说:“我想晓得天主是若何缔造那个世界的。对那个或阿谁现象、那个或阿谁元素的谱我其实不感兴趣。我想晓得的是他的思惟,其他的都只是细节问题。”
爱因斯坦对一个理论的美学要求到达了一种难以想象的地步。从麦克斯韦电磁学里发现的洛伦兹稳定性成了狭义相对论的核心,但是爱因斯坦觉得狭义相对论偏心惯性系,那点让他很不满。他觉得洛伦兹稳定性的范畴太窄了,天主不该该让那么美的思惟之局限在惯性系里,所以他要以一个在所有参考系里都成立的稳定性为前提,从头构造一个新的理论,那就是广义坐标稳定性和广义相对论的来源。
说白了,爱因斯坦就是觉得:那么好的对称性,那么美的设法,若是天主你不选用它做为构造世界的理论,那天主几乎就是瞎子。爱因斯坦坚信天主必然是用简单和美来构造那个世界的,所以我从如斯简单和美的对称动身构造的理论必然是有意义的。
杨振宁先生的档次,跟爱因斯坦几乎是一模一样的,那也是一位对理论的美学要求到达了难以想象地步的人。杨振宁先生最为崇拜的物理学家就是爱因斯坦,他对爱因斯坦倒置物理学的研究体例,把对称性放在极为重要的位置,以及对科学理论简单和美的逃求都有十分深入的融会。除此之外,杨振宁还有一个一般物理学家不具备的优势:他有一个十分凶猛的数学家老爹,那就使得杨振宁的数学程度比同时代的物理学家超出跨越良多。数学在现代物理中有多重要不消我多说,那就叫凭实力拼爹~
杨振宁先生是父亲杨武之是出名的数学家和数学教育家,是数学教育家就意味着他会以一种十分得当的体例让杨振宁接触并喜好数学。杨振宁仍是中学生的时候,他就从父亲那里接触到了群论的根底原理。诺特定理的发现让物理学家们重视对称性,但是他们对群论那种对称性的数学语言却没有足够的重视。其时良多物理学家都反对把群论那种过于笼统的数学语言引入到物理学里来,怼神泡利间接把群论嘲讽为“群祸”,薛定谔暗示附议,爱因斯坦也只是把群论当做一个细枝小节的工做。
幸运的是,杨武之刚好是擅长群论的数学家,他在清华大学开过群论的课程,其时华罗庚、陈省身那些将来的数学巨匠都来听过课。有如许的父亲,杨振宁对群论必定不目生,而杨振宁在西南联大学士论文的标题问题选的就是《群论和多原子分子的振动》,他的教师吴大猷就借此引导他从群论起头存眷物理学的对称性问题。
所以,年纪悄悄的杨振宁就已经十分重视物理学的对称性问题,而且在阿谁其他物理学家还在遍及思疑群论的年代,他已经很好的掌握了群论那种研究对称性的重要东西,那无疑长短常幸运的。有如许的杨振宁,他会对泡利在1941年颁发的那篇论文感兴趣是很天然的。
06对称性的推广我们把目光再拉回20世纪四五十年代,那时候人们已经晓得天然界除了电磁力和引力之外还有强力和弱力,强利巴量子和中子黏在一路(否则量子都带正电,同性相斥早就把原子核拆了),弱力在原子核衰变的时候阐扬感化(好比中子衰变酿成量子、电子和反中微子的β衰变)。但是那时候对强力和弱力的认识都还十分的浅薄,汤川秀树的介子理论、费米的四费米子理论都能只能解释强力、弱力的一些现象,还有大把的问题他们没法处理,谁都晓得那些理论只是关于强力、弱力的一个过渡理论,最初必定要被愈加切确的理论代替,但是该如何去寻找愈加切确的理论,各人心里也都没谱,没有一个非常明晰的思绪。
但是杨振宁先生那时候的思绪确是很明晰的:他对理论的美学要求是跟爱因斯坦一样苛刻的,因而,任何只是试图粗拙、唯象的模仿强力、弱力的理论他都懒得搭理(就跟爱因斯坦嫌弃它们长得丑一样)。然后,加上数学大牛的父亲和恩师吴大猷的悉心栽培,杨振宁那先生对数学的群论、物理学的对称性都有十分深入的理解,所以他就出格理解外尔那种设法的重要性。所以,他要不吝一切代价的扩展它。
外尔发现U(1)群整体标准对称性对应电荷守恒,但是,一旦我把那个整体对称性推广到局域,我就能够间接得到整个电磁理论。那种设法对物理学上有“洁癖”的杨振宁来说,吸引力其实是太大了,因为它其实是太美太简洁,给出的回报也太丰厚。若是我在强力、弱力里通过把某种标准对称性从整体推广到局域,是不是也能够得到关于强力、弱力的理论呢?
我们处置后诸葛亮的角度看,仿佛那一切都显得很天然,仿佛只如果物理学家都应该想到那个。但其实否则,且不说当爱因斯坦在搞同一场论的时候,他就已经被所谓的支流物理学界给边沿化了,外尔跟着爱因斯坦搞同一场论时提出的那种设法跟着被边沿化是很一般的工作。物理学家们每天都要产生各类各样的设法,那些设法哪些可靠,哪些值得考虑,哪些值得本身深切研究,哪些工具值得本身悍然不顾的去守护,那本来就是一个极困难的问题,也长短常考验物理学家程度的工作。
在其时更多物理学家的眼里,外尔如许的手法可能确实很标致,但有点“羊质虎皮”的嫌疑:麦克斯韦方程组我们早就晓得了,狄拉克、费曼等人也已经胜利的把电磁场量子化了(就是所谓的量子电动力学),你在电磁范畴如许颠来倒去仿佛确实很标致,但是没有增加任何常识啊?好吧,就算你的那个工具可能更普适,可能在强力、弱力里也有用武之地,但是在其时支流的描述强力和弱力的理论(也就是汤川秀树的介子理论和费米的四费米子理论)里,也看不到适宜的用武的处所。并且,一般物理学家对“对称决定彼此感化”的认识还远远没有到达爱因斯坦和杨振宁的程度,所以他们不怎么存眷那个也是天然的。
所以,其时除了杨振宁、泡利、外尔等寥寥几人存眷那个以外,其别人对此底子就不关心。而在那些存眷的人里,杨振宁又无疑是此中对此存眷度更高的一个,究竟结果本科论文就是做的那个,后来给他带来诺贝尔奖的宇称不守恒也是关于对称性的,他不断对对称性在物理学里的感化连结极高的存眷度。
既然想推广外尔的思惟,试图通过找到某种新的局域标准对称性来找到强力、弱力的理论,那么关键就是要找到那种对称性。但是怎么找那种对称性呢?当然仍是根据诺特定理,去看看强力、弱力里有什么守恒定律呗,更好仍是像电荷守恒那样,在那种彼此感化力特有的。
07同位旋杨振宁通过一番审查,发现弱彼此感化里暂时没有什么特殊的守恒定律,但是强彼此感化力里却有一个现成的:同位旋守恒。并且那个同位旋守恒还只在强彼此感化下守恒,在其它感化下纷歧定守恒,那不刚好么。
同位旋是啥呢?各人只要看一下量子(1.6726231 × 10^-27千克)和中子(1.6749286 ×10^-27千克)的量量,就会发现它们的量量其实是太接近了(不同在千分之一)。并且,人们还发现2个量子、1个量子1个中子、2个中子之间的强彼此感化几乎是不异的,也就是说,若是我们不考虑电磁感化,在强彼此感化的眼里,量子和中子完满是不异的。
于是,海森堡就来了提出了一个斗胆的设法:他认为量子和中子压根就是统一种粒子-核子的两种差别的形态,它们配合构成了一个同位旋二重态。在笼统的同位旋空间里,量子能够“扭转”成为中子,中子也能够“扭转”成为量子,因为量子和中子在强彼此感化下是一样的,所以,我们就能够说:强彼此感化具有同位旋空间下的扭转稳定性。
各人可能留意到我上面的“扭转”打了一个引号,因为我们那里说的扭转并非在我们常说的实在空间里,而是在核子内部笼统出来的同位旋空间,因而那种对称性又叫内部对称性,而之前我们谈的各类跟时空有关的对称性就叫外部对称性。内部对称性咋一看仿佛不那么实在,但其实它跟外部对称是一样实在天然的,它们一样对应着守恒定律,强彼此感化下同位旋空间里的那种扭转稳定性就对应同位旋守恒。
关于同位旋的工作那里就不再多说了,各人只要晓得在强彼此感化里同位旋是守恒的,而且同位旋空间下量子和中子能够彼此扭转得到就行了。
因为描述对称性的数学语言是群论,与同位旋那种对称相对应的群叫SU(2)(特殊幺正群),里面的数字2提醒我们那是两个物体(如量子和中子)彼此变更来确定的。我们也先甭管那个SU(2)群到底是什么意思(那是群论的根底常识,感兴趣的本身看群论),只需要晓得那个群能够描述两个物体彼此变更的那种对称性,跟电磁理论里用U(1)群来描述电磁理论里的对称性一样的就行了。
外尔和泡利发现,只要我们要求系统具有U(1)群的局域标准稳定性,我们就能从中推导出全数的电磁理论。那么,杨振宁若是认为强力的素质由量子和中子彼此感化产生,那么推广前面的思惟,我们就应该要求系统具有SU(2)群的局域标准稳定性。
好吧,要推广那就推广吧,不就是把局域标准稳定性从U(1)群推广到SU(2)群么,有些人认为科学家们风风雨雨什么没见过,把一个工具从U(1)群推广到SU(2)群应该没什么难度吧?那你就错了,那玩意还实不是那么简单的,广义相对论也不外是把狭义相对论里的洛伦兹稳定性推广到了广义坐标稳定性,你觉得那个简单么?
U(1)群的问题之所以比力简单,是因为跟U(1)群对应的电磁理论它自己就具有局域标准对称性。也就是说,当我们的麦克斯韦同窗写下麦克斯韦方程组的时候,他就已经把U(1)群的局域标准对称性写到那方程里去了,固然他本身没有意识到。熟悉电磁理论的人都晓得其实我们有两套表述电磁场的系统,一套就是我们初中就起头进修的场强系统,还有一套势系统,也就是电磁势那些工具,从那个角度很容易就能看出它的标准稳定性。
但是SU(2)那里一切都是空白,没有电磁势如许的工具。杨振宁先生想做的就是要找到类似电磁势那种具有局域标准稳定性的工具,然后操纵他们来描述强力,所谓的推广是那个样子的一种推广。在那种推广里,最困难的处所就在那四个字:非阿贝尔。
08非阿贝尔群在前面我跟各人提过,杨-米尔斯理论又叫非阿贝尔标准场论,那个阿贝尔指的是阿贝尔群(以挪威的天才数学家阿贝尔定名),它又叫交换群,通俗的讲就是那个群里的运算是满 *** 换律的。

最简单的例子就是整数的加法,小学生都晓得加法满 *** 换律:3+5=5+3,不管你加数的挨次怎么交换,最初的成果都稳定。于是,我们就说整数和整数的加法构成了一个整数加法群,那个群的运算(加法)是满 *** 换律的,所以那个整数加法群就是阿贝尔群。
那么,非阿贝尔群天然就是指群的运算不满 *** 换律的群。那么,不满 *** 换律的运算有没有呢?当然有了,最常见的就是矩阵的乘法。略微有点线性代数根底的人都晓得:两个矩阵相乘,交换两个矩阵的位置之后得到的成果是纷歧样的。而矩阵那种工具在数学、物理学里长短常根底的工具,好比你对一个物体停止扭转操做,最初都能够转化为物体跟一个扭转矩阵的运算,如许非阿贝尔其实就没啥奇异的了。
那里我借用一下徐一鸿在《可畏的对称》(强烈安利那本书,需要的在回复“可畏的对称”即可)里的一个例子让各人感触感染一下那种不成交换的次序,也就长短阿贝尔的觉得。
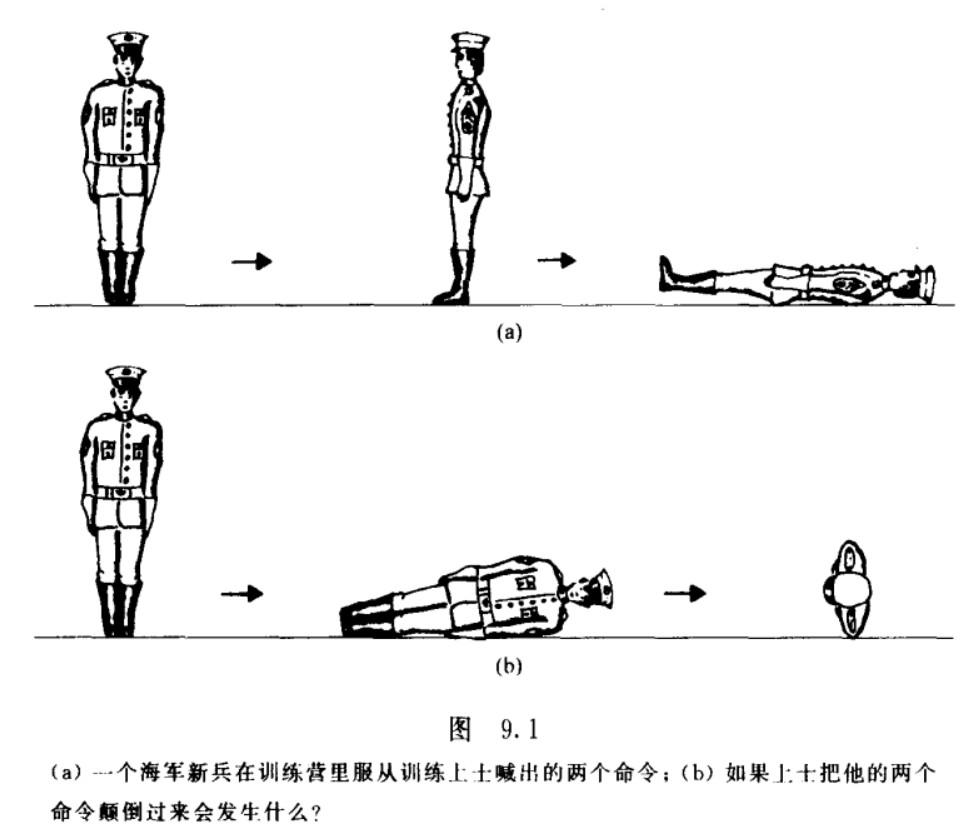
上图是一个新兵,他如今要施行两个操做,一个是顺时针扭转90°(从上往下看),一个是向右倒(其实就是从外往里看顺时针扭转90°)。上面的a图是先扭转再右倒,而下面的b图则是先右倒再扭转,我们能够清晰的看到,最初那两小我的形态是完全纷歧样的(一个左侧对着你,一个头对着你)。
形态纷歧样申明什么呢?申明那两个扭转操做若是改动先后次序的话,得到的成果是纷歧样的,而那两个扭转操做都能够通过跟两个矩阵相乘得到,那说矩阵的乘法是不克不及随意交换挨次的。
好了,有了那些概念,我们再回到杨振宁先生的问题上来。
09杨-米尔斯理论外尔把U(1)群的整体标准对称性推广到了局域,因为U(1)群(1×1矩阵)是阿贝尔群,所以那个过程很简单;杨振宁试图把SU(2)群的整体标准对称也推广到局域,但SU(2)群(2×2矩阵)长短阿贝尔群,那个就费事了。
我们晓得杨振宁先生的数学程度在物理学家群体里长短常高的,他的父亲杨武之就是群论巨匠,他本身也很早就进入了对称性范畴。饶是如斯,他从泡利1941年的论文起头,前前后后过了十几年,不断到1954年,他才和米尔斯(其时和杨振宁先生在统一间办公室,是克劳尔传授的博士研究生)一路写出了划时代的论文《同位旋守恒和同位旋标准稳定性》和《同位旋守恒和一个推广的标准稳定性》。

上图即是1954年杨振宁和米尔斯在《物理评论》上颁发的之一篇论文截图。根据老例,那种典范论文长尾科技会提早给各人找好,想亲眼目击一下杨振宁先生那篇划时代论文的,回复“杨米尔斯理论论文”就行。
那两篇论文正式宣告了杨-米尔斯理论的降生,杨振宁先生末于把局域标准对称的思惟从阿贝尔群推广到了更一般的非阿贝尔群(阿贝尔群的电磁理论成了它的一个特例),从而使得那种精妙的标准对称能够在电磁理论之外的六合大展拳脚,也使得他不断对峙的“对称决定彼此感化”有了落脚之地。为了区别起见,我们把外尔的那一套理论成为阿贝尔标准场论,把杨振宁和米尔斯提出来的称为非阿贝尔标准场论,或者间接叫杨-米尔斯理论。
杨-米尔斯理论给我们供给了一个切确的数学框架,在那个框架里,只要选择了某种对称性(对应数学上的一个群),或者说你只要确定了某个群,后面的彼此感化几乎就被完全确定了,它的标准玻色子的数目也完全被确定了。那就是为什么后来各人能间接从强力和弱电理论里预言那么多还未被发现的粒子的原因。

什么是标准玻色子?科学家们根据自旋把根本粒子分红了费米子(自旋为半整数)和玻色子(自旋为整数),此中费米子是构成我们根本物量的粒子,好比电子、夸克,而玻色子是传递感化力的粒子,好比光子、胶子。有些人可能是之一次传闻传递感化力的粒子那种说法,会觉得十分奇异,怎么感化力还用粒子传递?
没错,在量子场论里,每一种感化力都有专门传递感化力的粒子。好比传递电磁力的是光子,传递强力的是胶子,传递弱力的是W和Z玻色子,传递引力的是引力子(不外引力子还没有找到)。两个同性电子之间为什么会彼此排挤呢?因为那两个电子之间在不断的发射交换光子,然后看起来就像在彼此排挤,那就跟两小我在溜冰场上互相抛篮球然后都向撤退退却一样的事理。那么彼此吸引就是朝相反的标的目的发射光子了,其他的力也都是一样,那些传递彼此感化的玻色子在标准场里都通盘被称为标准玻色子。
也就是说,在杨-米尔斯理论里,那些传递彼此感化的粒子都叫标准玻色子,每一个群都有跟他对应的标准玻色子,只要你把那个群确定了,那些标准玻色子的性量就完全确定了。好比在U(1)群里,标准玻色子就只要一个,那就是光子;在SU(3)群里,理论计算它的标准玻色子不多很多就是8个,然后尝试物理学家就按照那个去找,然后实的就找到了8种胶子。以前是尝试物理学家发现了新粒子,理论物理学家要揣摩着怎么去解释,如今是理论物理学家预测粒子,尝试物理学家再去找,爱因斯坦倒置研究物理的办法如今末于从门路成了支流。
10从杨-米尔斯理论到尺度模子杨-米尔斯理论从数学上确定了“对称决定彼此感化”,那么我们接下来的问题就是“什么样的对称决定什么样的彼此感化”了。好比,我如今要描述强力,那么强力到底是由什么对称决定的呢?
有些人可能觉得奇异,你上面不是说了一大片同位旋守恒么,杨振宁先生不就是看到同位旋守恒和电荷守恒的类似性才最末提出了杨-米尔斯理论么,为什么如今还要来问强力是什么对称决定的,莫非不是同位旋么?
没错,还实不是同位旋!
海森堡从量子和中子的量量附近提出了同位旋的概念,同位旋守恒确实也只在强力中成立,但是各人不要忘了量子和中子的量量只是接近,并非相等。杨-米尔斯理论里的对称是一种切确对称,不是你量子和中子的那种近似相等,其时的科学家们把量子和中子的细小量量不同寄希望于电磁污染,但事实并不是如斯。所以,当杨振宁试图用量子中子同位旋对称对应的SU(2)群做为强力的对称群的时候,得到的成果必定跟现实情况不会相符的。
但是,我们要留意到其时才1954年,人们对强力的认识还太少了,后来我们晓得实正决定强力的切确对称是夸克的色对称,与之对应的群是SU(3)群,所以我们把最末描述强力的理论称之为量子色动力学(QCD)。但是,夸克那个概念要到1964年才由盖尔曼、茨威格提出来,所以杨振宁在1954年就算想破脑袋也不成能想到强力是由夸克的色对称决定的。
夸克有六种(上夸克、下夸克、奇夸克、粲夸克、底夸克、顶夸克),每一种夸克也称为一味,量子和中子之间的细小量量差别是就是因为上夸克和下夸克的量量差别。别的,每一味夸克都有三种色(红、绿、蓝),好比上夸克就有红上夸克、绿上夸克和蓝上夸克,那差别色的同种夸克之间量量是完全相等的,那是一种完全切确的对称,那种色对称最初决定了强彼此感化。
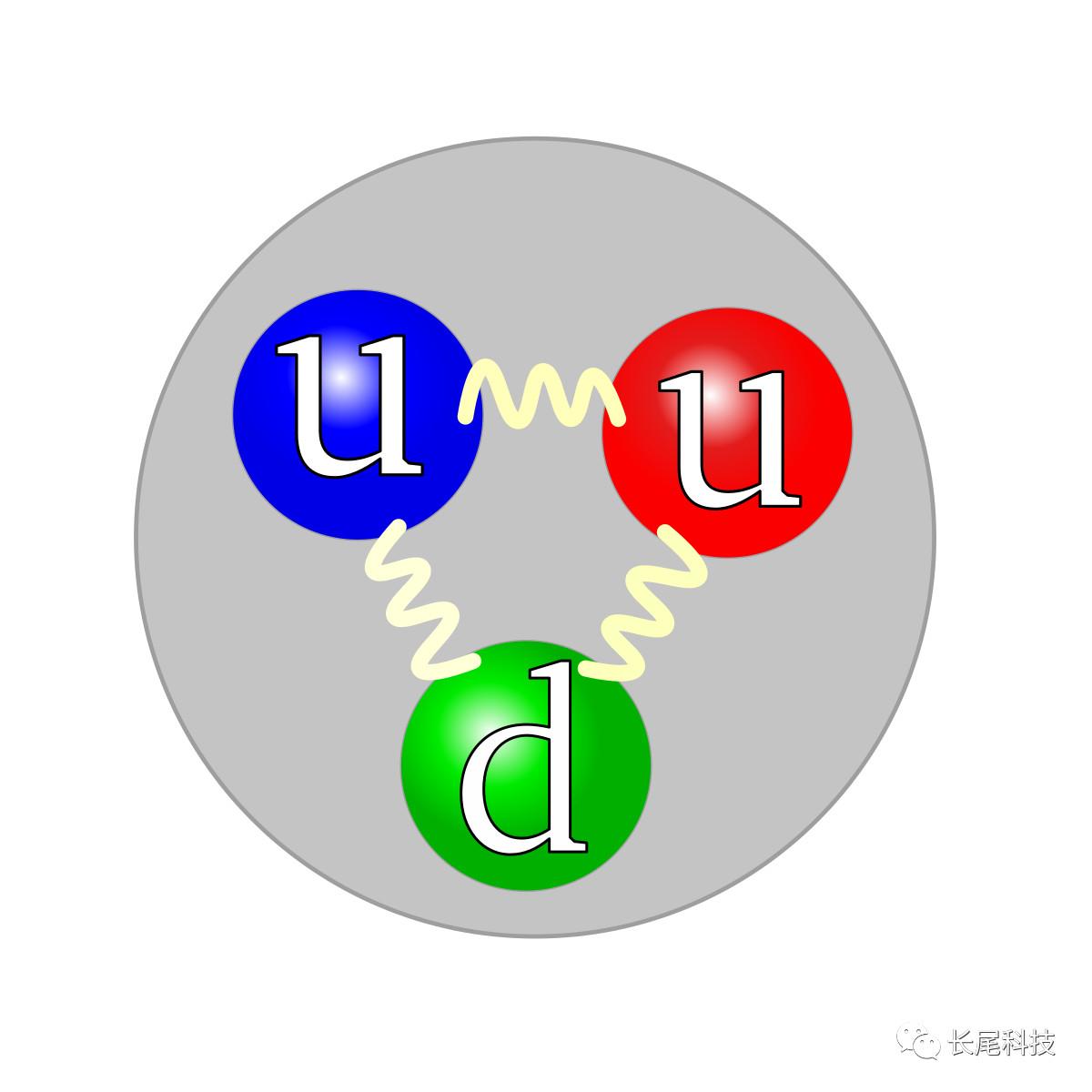
一旦成立了那种夸克模子,而且意识到夸克色对称那种切确对称对应SU(3)群,那么接下来操纵杨-米尔斯理论去构造描述强力的理论就长短常简单的工作,根本上就是带公式套现成的事。所以,胜利描述强力的量子色动力学的核心就是夸克模子+杨-米尔斯理论。
在弱力那边情况也是类似的,你要想找到描述弱力的理论,那就先去找到决定弱力的切确对称和响应的群,然后间接根据杨-米尔斯理论来就行了。但是,弱力那边的情况略微复杂一点,科学家们没找到什么弱力里特有的切确对称,但是他们发现,若是我把弱力和电磁力同一起来考虑,考虑同一的电弱力,我却是能发现那种切确对称。于是,他们索性不去零丁成立描述弱力的理论了,转而间接去成立同一弱力和电磁力的弱电同一理论。而最初在弱电彼此感化中实正起感化的是(弱)同位旋——超荷那个工具,他们对应的群是SU(2)×U(1)(×暗示两个群的曲积)。
描述强力的量子色动力学和描述电磁力和弱力的弱电同一理论一路构成了所谓的粒子物理尺度模子,于是我们能够在杨-米尔斯理论那统一个框架下描述电磁力、强力和弱力,那是物理学的伟大成功。同时,我们也要清晰的晓得,杨-米尔斯理论不等于尺度模子(没有夸克模子你拿着理论也不晓得怎么用),它是一个数学框架,是一把神兵利器,它自己其实不产生详细的理论常识,但是一旦你把它用在适宜的处所,它就能给你带来超出想象的回报(想想我们50年代末还对强力衰力一筹莫展,但是70年代末就完全征服了它们)。
11不能不说的量量问题尺度模子的成立是另一个十分宏大的故事,那里就不多说了,那里谈一个不能不说的问题:量量问题。
在上面我们晓得了费米子是构成物量的粒子,玻色子是传递彼此感化力的粒子。好比两个电子之间通过交换光子来传递电磁力,两个夸克通过交换胶子来传递强力,那么光子和胶子就别离是传递电磁力和强力的标准玻色子。但是,各人有没有考虑过玻色子的量量问题?若是传递彼此感化力的玻色子量量过大或者过小会咋样?

仍是以溜冰场传球为例,假设两小我站在溜冰场上彼此传篮球,那么一起头他们会因为篮球的冲力然后退(那就是斥力的表示),从而把间隔拉开,但是他们会不断如许渐渐撤退退却下去么?当然不会!当两人之间的间隔足够远的时候,你投篮球底子就投不到我那里来了,那我就不会撤退退却了。再想一下,若是你投的不是篮球而是铅球那会如何?那可能我们还在很近的时候,你的铅球就投不到我那里来了。
在溜冰场的模子里,球就是传递感化力的玻色子,你无法接到球就意味着那个力无法传到你那里来,就是说它的力程是有限的。从篮球和铅球的比照中我们也能清晰的晓得:玻色子的量量越大,力程越短,量量越小,力程越长,若是玻色子的量量为零,那么那个力程就是无限远的。
所以,为什么电磁力是长程力,能传布很远呢?因为传递电磁力的光子没有量量。但是我们也清晰的晓得,强力和弱力都仅仅局限在原子核里,也就是说强力、弱力都是短程力,所以,根据我们上面的阐发,那么传递强力和弱力的玻色子似乎应该是有量量的,有量量才气对应短程力嘛。
但是,杨振宁在研究标准场的时候,他发现要使得系统具有局域标准稳定性,那么传递感化力的标准玻色子的量量就必需为零。也就是说,标准玻色子若是有量量,它就会毁坏局域标准对称性。
为什么局域标准对称性要求玻色子的量量必需为零呢?你能够如许想,什么叫局域标准对称?那就是差别的处所在做着差别的变更,既然差别的处所变更是纷歧样的,那么必定就必需有个中间的信使来传递那种形态,如许各人才气协调工做,否则你跳你的我跳我的岂不是乱了套?好,既然那个信使要在差别处所(也可能是两个十分远的处所)传递形态,根据上面的阐发,它是不是应该零量量?只要量量为零才气跑的远嘛~
所以,如许阐发之后,我们就会发现局域标准对称性和标准玻色子零量量之间的对应关系长短常天然的。但是,如许就形成了如今的窘境:局域标准对称性要求标准玻色子是零量量的,但是强力、弱力的短程力事实似乎要求对应的标准玻色子必需是有量量的,怎么办?
那个问题不只困扰着杨振宁,它也同样困扰着泡利(其实其时对标准场感兴趣的也就他们寥寥几个)。泡利起头对标准场的工作也很感兴趣(杨振宁就是读了泡利1941年的那篇论文才起头对标准场感兴趣的),但是当泡利发现了那个似乎无解的量量问题之后,他就渐渐对标准场失去了兴趣,也就没能得出最初的方程。
杨振宁的情况略微纷歧样,他的数学功底十分好,对群论的深切理解可以让他更深入的理解对称性的问题(想想那会儿物理学家都不待见群论,泡利还带头把群论称为群祸)。别的,在美学思惟上,杨振宁是爱因斯坦的铁杆粉丝,他们都是“对称决定彼此感化”坚决撑持者,那使得杨振宁对标准场产生了谜之喜欢。并且,杨振宁那会儿才30岁摆布,是科学家精神和缔造力的巅峰期间,天然无所畏惧。
所以,杨振宁不断在疯狂地寻找杨-米尔斯方程,找到方程之后,即使晓得有尚未处理的量量问题,他仍然决定颁发他的论文。在他眼里,那个方程,那套理论是他心里“对称决定彼此感化”的完美代表,他跟爱因斯坦一样坚信天主喜好简洁和美,坚信天主的简单和美是由切确对称决定的。若是是如许,那么还有什么比基于标准稳定性那种深入对称的杨-米尔斯理论更能描画天主的思惟呢?
杨振宁对对称性的深入理解使得他对杨-米尔斯理论有十分强的自信心,至于强力、弱力上表示出来的量量问题,那不外是那个理论在应用层面呈现了一些问题。强力、弱力比电磁力复杂良多,因而用杨-米尔斯理论来解释强力、弱力天然就不会像处置电磁力那样简单。为什么电磁力那么简单?你想想,电子有电效应,电子的运动产生磁效应,电子之间的彼此感化是通过光子那个标准玻色子传递的,所以电磁力的素质就是电子和光子的彼此感化。那里只要一个粒子电子,和一个标准玻色子光子,并且光子仍是没有量量的,你再看看强力里面,三种色夸克,八种差别的胶子,那铁定比电磁力复杂多了啊!
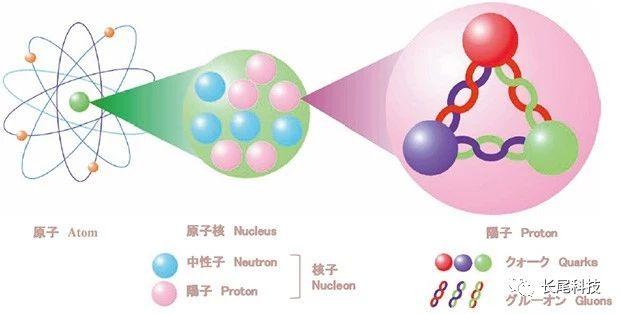
所以,杨振宁想的是:杨-米尔斯理论没问题,如今它应用在强力衰力上呈现了一些问题(量量问题就是初期更大的一个),那也是天然的。那些是问题,而非错误,以后跟着人们研究的深切,那些问题应该能够渐渐得到处理的。
汗青的开展确实是如许,量量问题后来都通过一些其他的手段得到领会决,那么量量问题最末是怎么处理的呢?
在描述强力的量子色动力学里,我们留意到传递夸克间感化力的胶子原来就是零量量的,零量量跟标准对称性是相容的。那但是,若是如许的话,零量量的玻色子应该对应长程力啊,为什么强力是短程力(只在原子核里有效)呢?那就涉及到了强力里特有的一种性量:渐近自在。渐近自在说夸克之间的间隔很远的时候,它们之间的感化力十分大,一副谁也不克不及把它们分隔的架势,但是一旦实的让它们在一路了,间隔很近了,它们之间的彼此感化力就变得十分弱了,仿佛对面那个夸克跟它没任何关系似的,活脱脱的一对夸克小情侣。如许在量子色动力学里,零量量的标准玻色子就和强力的短程力没有抵触了。
渐近自在解释了为什么胶子是零量量但是强力确是短程力,那么传递弱力的W和Z玻色子可是有量量的。有量量的话短程力是好解释了,但是我们上面说有量量的标准玻色子会毁坏标准对称性,那标准对称性可是杨-米尔斯理论的根底啊,它被毁坏了那还怎么玩?
最初处理那个问题的是希格斯机造。希格斯机造是来打圆场的:你杨-米尔斯理论要求标准玻色子是零量量的,但是最初我们丈量到W和Z玻色子是有量量的,怎么办呢?简单,我认为W和Z那些传递弱力的标准玻色子一出生的时候是零量量的,但是它来到那个世界之后渐渐因为某种原因获得了量量,也就是说它们的量量不是生成的而是后先天予的,如许就既不与杨-米尔斯理论相抵触,也不跟现实丈量相抵触了。
所以,希格斯机造其实就是付与粒子量量的机造。它认为我们的宇宙中四处都充满了希格斯场,粒子若是不跟希格斯场发作感化,它的量量就是零(好比光子、胶子),若是粒子跟希格斯场发作感化,那么它就有量量,发作的感化越强,得到的量量就越大(需要申明的是,并非所有的量量都来自于粒子和希格斯场的彼此感化,还有一部门来自粒子间的彼此感化)。2012年7月,科学家末于在大型强子对碰机(LHC)中找到了希格斯粒子,为那段故事画上了一个圆满的句号,也天经地义地预约了2013年的诺贝尔物理学奖。

如许杨-米尔斯理论就能够完好的描述强力、弱力和电磁力了,在霍夫特完成了非阿贝尔标准场的重整化(重整化简单的说就是让理论能算出有意义的数值,而不是无限大那种没意义的成果,那是点粒子模子经常会呈现的问题。举个最简单的例子,我们都晓得电荷越近,它们之间的电磁力越大,那么当电荷的间隔趋近于零的时候,莫非电磁力要酿成无限大么?那个当做思虑题~)之后,粒子物理尺度模子就正式投产商用。
12结语至此,我们关于杨-米尔斯理论的故事就告一段落了,相信能对峙看到那里的人对杨-米尔斯理论应该都有了个大致的领会,对它的感化和意义也会有本身的判断。
那篇文章是我有史以来消耗心血最多的科普文,为此我的公家号都有好长一段时间没更新了,在公家号后台和社群里也都天经地义地收成了一 *** 粉丝的催更~不外,相信各人看完那篇文章之后应该就能理解了:杨-米尔斯理论涉及的工具其实是太多了,对称性、标准场、非阿贝尔群、尺度模子,那些工具关于许多非物理专业的同窗来说其实是太目生了,以至历来都没传闻过。即使关于物理系的学生,杨-米尔斯理论也是要到研究生阶段才接触的工具。因而,要把那么复杂,牵扯面那么广的工具用中学生能懂的语言科普出来,此中难度可想而知。许多公式和术语跑到嘴边又被我逼归去了,出格要在不涉及阐发力学和感化量的前提下讲杨-米尔斯理论,差点没给我逼出内伤~
之所以执意用那么通俗的语言讲杨-米尔斯理论,次要就是想让更多人愈加客不雅的理解杨振宁先生的工做,良多工作若是彻底搞清晰了,就会省去良多无意义的争论。如今网上关于杨振宁先生的新闻良多,但是很不幸,大部门新闻上的却是娱乐版,即使除去那些娱乐八卦,关于杨先生科学方面的话题大部门最初都演酿成了诸如“杨振宁实的很伟大么?”“杨振宁跟霍金谁凶猛?”“杨振宁跟爱因斯坦一样伟大吗?”“杨振宁没有你想象的那么伟大!”等极容易引起撕逼骂战却又很浮泛没营养的问题。而且,论战中的两边要么就把杨振宁先生往天上捧,要么就把他使劲往地上踩,那还算是科学讨论么?那是讨论科学问题该有的立场么?
物理学家并非擂台上的拳击手,他们一路共同努力构建我们如今恢弘的物理大厦。没有开普勒和伽利略的奠定,不成能有牛顿的力学系统;没有法拉第工做,不成能有麦克斯韦的电磁大厦;狭义相对论在20世纪初已经是水到渠成呼之欲出了,爱因斯坦也只不外是捷足先登了罢了。并且,除了广义相对论确实是爱因斯坦的独门首创,仿佛还实没有哪个工具说长短谁不成的。没有牛顿,我估量胡克和哈雷也快找到万有引力定律了,洛伦兹和彭加莱已经一只脚跨入狭义相对论的大门了,有没有爱因斯坦狭义相对论差不多都该呈现了。
我那么说并非要否认牛顿和爱因斯坦他们的功绩,能抢在同时代最出色的思维之前发现那些理论,那自己就是科学家的才能表现。我只是想建议各人不要总把留意力放在“谁或者谁更伟大,谁比谁更凶猛”那种很虚的工具上面,而更多的把留意力放在那些科学家工做自己上去,那些才是全人类配合的贵重财产。各人的时间都很贵重,我们就尽量把时间都花在刀刃上去,科学家最贵重是他们的科学思惟,而中国比任何一个国度都不贫乏娱乐八卦。
杨振宁先生是我们国宝级的科学家,杨-米尔斯理论是他工做里目前已知的最为灿烂的明珠(鉴于杨振宁先生工做的根底性和前瞻性,他有良多理论刚提出来的时候不被重视,过了几十年之后却发现它极为重要,所以我不确定以后能否会呈现比杨-米尔斯理论更重要的工具)。
诺特发现了对称性和守恒律之间的关系,翻开了现代物理对称性的大门。
爱因斯坦灵敏而深入的意识到了那点,然后以雷霆之势将它应用在相对论上,获得的庞大胜利把其时其他的科学家惊得目瞪口呆。但是那个套路爱因斯坦熟悉,其别人不熟啊,况且在量子革命的时代,爱因斯坦是那帮量子革命家的“背面教材”,波尔才是他们的教皇,所以人家也不屑于跟你玩。
杨振宁能够说是爱因斯坦的嫡派门生,若是说爱因斯坦对对称性是偏心的话,那么杨振宁对对称性就是情有独钟了。他充实吸收了爱因斯坦的对称思惟,而且把它发扬光大,再吸收了外尔的标准对称的思惟,最初缔造了集大成的杨-米尔斯理论。杨-米尔斯理论出来以后,对称性就不再是一小我的玩具了,杨振宁通过那个理论把对称性那种高峻上的精英产物一会儿酿成了谁都能够玩的布衣玩具,他把若何释放对称性里储藏能量的体例给尺度化、东西化、流水化了。从此,“对称决定彼此感化”就不再是一句口号,而成了物理学家们的共识和最根本的指点思惟,那极大的释放了物理学家的消费力,为后来快速构建尺度模子奠基了根底。
那一块是各人在议论杨振宁先生的工做,议论杨-米尔斯理论的时候最容易忽略的一块,若是你不克不及认识到对称性在现代物理里的重要性,不克不及认识到杨振宁先生和杨-米尔斯理论在对称性问题上的感化,那么你对杨先生工做的理解长短常全面的,以至错失了他最精华的部门。希格斯机造、渐近自在、夸克禁闭、自觉对称破缺、标准场的重整化,那些从杨-米尔斯理论到尺度模子之间浩瀚出色纷呈的故事似乎更合适平话,但是,各人要记住对称性才是现代物理的核心。

杨振宁先生长短常伟大的物理学家,除了在学术上获得的庞大成就以外,他的治学立场一样非常值得各人去深切进修。深切领会之后你能十分明显的觉得到杨先生身上同时闪灼着中国教育和西方教育的长处,他十分有效的把工具方教育里的糟粕都给躲避了,所以杨先生老是能很超前的看到一些关键问题。学术上的问题我们无法复造,但是科学教育中一些问题我们是能够复造的,那些问题我后面会渐渐跟各人谈。
杨振宁先生在八九十岁的时候还亲身给清华大学的本科生上课(羡慕嫉妒恨~),想必也是想把本身做学问一些心得尽可能的交给更多人,那点跟我们那些做科普的设法是一样的。考虑到杨先生的年龄,长尾君不能不写个大大的“服”,不晓得以后本身七老八十了,还有没有给年轻人做科普的动力~
最初,祝杨先生身体安康~
相关文章:
原文链接:
相关册本:若是那篇文章让你对杨-米尔斯理论和标准场论产生了兴趣,你想进一步领会杨振宁先生的相关工做,那能够看看下面的册本。
1、必看:《可畏的对称》(徐一鸿)那本书没什么好说的,若是你喜好那篇文章,那那本书就是必看册本。那是一本严峻被低估,以至差点绝版的关于对称性的绝佳科普书。做者徐一鸿本人就是处置那方面工做的物理学家,此书的专业性不消思疑,别的他的文笔你也不消担忧,也很通俗。
以前的理论物理科普次要集中在相对论、量子力学、黑洞、宇宙、超弦等内容上,关于对称性在物理学中感化的科普十分少。所以,我们遍及对20世纪40年代以来粒子物理范畴的开展比力目生,所以对杨振宁先生的工做就比力目生,那本书填补了那个空白。
理解科学丛书·可畏的对称:探寻现代物理学的斑斓 京东 ¥31.00 去购置 2、进一步领会:《粒子物理导论》(格里菲斯)若是你觉得科普书的深度不敷,想再进一步领会对称性和粒子物理的相关内容,我保举你看看格里菲斯的那本《粒子物理导论》。
那本书名义上是一本教材,但是我却始末把它看做半科普半教材的一本书。因为,相对科普书,它的深度和难度必定是高了一级,但是,相对正儿八经的粒子物理或者量子场论的教材,它的难度又明显低了好几个品级,那就是格里菲斯的凶猛之处了。
他老是能用十分通俗的语言,十分顺畅的逻辑把物理讲得很清晰。所以,他的书都出格受初学者欢送,十分合适用来做入门,十分合适从科普到教材的过渡。格里菲斯有出名的三部曲,除了那本以外,还有《量子力学概论》和《电动力学导论》都是各自范畴更好的入门教材。可惜,后面两本仿佛都绝版了!!!
粒子物理导论(翻译版·原书第2版) 京东 ¥79.00 去购置看完那本书以后,若是你还想做更进一步的领会,那就只要看专业的量子场论的教材了。那类教材一般都是英文的,诸如A.Zee(就是《可畏的对称》的做者徐一鸿)、Peskin 、Srednicki、Weinberg等等,它们详细的书能够参考那个答复:若何评价 Zee, Srednicki, Schwartz 和 Peskin 的量子场论教材?
3、同一理论:《爱因斯坦与万物之理:同一路上的人和事》我在文章的一起头就讲了一部极简的物理学同一史:牛顿同一了天上和地上的力,麦克斯韦同一了电、磁、光,爱因斯坦同一了牛顿力学和麦克斯韦电磁学,趁便也处理了引力,以杨-米尔斯理论为根底的尺度模子同一了电磁力、强力和弱力。
若是各人对物理学的同一史很感兴趣,想进一步领会同一路上的各类工作,我就保举张天蓉教师的那本《爱因斯坦与万物之理:同一路上的人和事》。张天蓉教师跟徐一鸿一样,也是相关专业的物理学家,所以,她书里的数学,或者比力难的物理思惟会讲得更深一些,但是绝对仍是科普的层面。
好比,她讲狄拉克推导狄拉克方程的时候,是实的会用很通俗的语音把狄拉克推方程的思惟和过程说出来。她实的会用详细的例子给你讲群论的思惟,将标准场的思惟是若何一步步成立的,实的会把张量、度规张量、黎曼张量放在科普的层面给你讲,那是良多科普书不会涉及到的深度。
因而,若是你看一半的科普书觉得深度不敷,又不想去看专业的数学书,只想领会一下此中的重要思惟,那么那本书能够看看。
爱因斯坦与万物之理:同一路上人和事 京东 ¥29.30 去购置 4、杨振宁先生的书和列传:《杨振宁传》+《晨光集》+《曙光集》想进一步领会杨老的事迹,那就去看他的列传吧,那里我保举杨建邺的那本《杨振宁传》,里面杨老的生安然平静科学思惟都做了不错的介绍。
杨振宁传(增订版)(二版) 京东 ¥45.70 去购置此外,还有杨振宁先生本身出的《晨光集》和《曙光集》,书中收录了一些杨老的代表性文章,也有亲朋、学生、同事等人写的回忆文章。那并非杨老的学术论文集,一般人都可以看的懂的,从那书名里也能看出杨老对将来年轻人的希望~
晨光集 京东 ¥48.70 去购置 曙光集(十年增订版) ¥69.30起 相关答复:
我出的书:
什么是高中物理 京东 ¥29.90 去购置