为什么静电计能够测电压？

·起首先介绍静电计与电压关系定性的理论

静电计张角反响的其实是转移给静电计的电量，当静电计和带电体接触的时候，带电体味把电荷传给静电计金箔一部门，最末招致静电计金箔与带电导体静电平衡、电势相等，一般情况下，静电计的电容会很小，因而转移给静电计的电荷其实不多，不会引起导体电势过大的改动，如许一来最末静电平衡静电计金箔的电势照旧是带电导体的初始电势，咱们设为V。若是假设静电计的电容在偏转过程中不发作太大变革的话（布劳恩静电计的电容现实会增加，不外增长速度不及电量，阐发在后面），那么静电计电势V越大，转移到静电计身上的电量就越大，从而静电计偏转角也越大。

按照尝试和理论计算：金箔静电计的张角与电势并非反比关系，但至少是严酷单调递增的关系，关于那种定性的关系，上面已经做了介绍；关于静电计构造复杂的静电计，若是很难做出严酷单调性申明的话，能够分为两步。1.能够利用静电起电机给金箔静电计充电，通过金箔验电器的偏转角不竭减小，证明带电体电荷量在空气中会不竭衰减；2.然后再把充好电的莱顿瓶与复杂静电计连在一路，我们若是发现：放着莱顿瓶不管，复杂静电计偏转角会逐步减小的话，那么因为上一个尝试证了然带电体在空气中会放电、电荷量会减小，而且因为莱顿瓶构造稳定，所以莱顿瓶电容是确定的，电量在减小申明其电势在降低，那么那也就证了然复杂静电计的偏转角会跟着莱顿瓶电势差的下降而下降，那也就能够用来证明复杂静电计的严酷单调递增关系的办法；

但是卡文迪许的通草球静电计和麦克斯韦和开尔文的汤姆逊象限静电计都是近似线性的，伏打的稻草静电计在25度的丈量范畴内都能够与电压连结线性的关系！

伏打的稻草静电计·下面介绍一下若何确定静电计偏转角和电压的定量关系 1.早期静电计的定量研究 1.1.通草球静电计

通草球静电计是卡伐洛(T. Cavallo)于1777年创造的，是对亨雷静电计的改良。关于对通草球静电计，验证电压与偏转角线性关系的卡文迪许的尝试，以及伏打的电容金叶静电计测电压的办法，我在那篇文章里讨论过（因为在欧姆定律的验证中静电计会起关键感化，所以在那篇文章里我先讨论了静电计丈量的问题）。我再解释一遍好了。

既然电压表是按照欧姆定律造的那欧姆一起头怎么发现电流跟电压成反比？10 附和 · 6 评论答复

“因为卡文迪许发现若是给一个莱顿瓶两极别离带上2个单元电量，静电计测得偏转角是2个单元；若两个不异莱顿瓶并联，两极别离带2个单元电荷，静电计偏转一个单元；按照尝试静电计偏转角减半；能够阐发因为两个不异莱顿瓶并联让电容扩大到本来两倍，电量稳定，而按照C=Q/U，电势差减半；因为电势差减半的同时，通草球静电计偏转角减半，因而偏转角反比于电势差。”（那个尝试后来伏打改用亨雷静电计也做过研究，伏打还研究了棒状电容器的并联）(其实那个线性成果只是近似的，若是角渡过大，就会呈现非线性)

I. 卡伐洛通草球静电计；II. 本纳特金叶验电器

关于卡伐洛静电计，能够根据电势与偏转角的以下关系，对电压实现绝对丈量：

V=2lsinθkmgtanθRV=\frac{2lsin\theta\sqrt{kmgtan\theta }}{R}

理论推导：卡伐洛静电计是两个小球在静电力 静F静F_{静} 、拉力F和重力mg的感化下平衡。我们设卡伐洛静电计的偏转角是 2θ2\theta ，因而悬挂小球的丝线与铅垂线的夹角就是 θ\theta ，我们设丝线长度为l。从而对力停止正交合成能够得到： 静Fsinθ=F静Fsin\theta=F_{静} ， Fcosθ=mgFcos\theta=mg ，所以 静F静=mgtanθF_{静}=mgtan\theta 。按照对称性，可知两个小球的电量相等，因而按照库伦定律， 静F静=kq2/r2=kq2/(2lsinθ)2F_{静}=kq^{2}/r^{2}=kq^{2}/(2lsin\theta)^{2} ，联立上面的成果能够得到： kq2/(2lsinθ)2=mgtanθkq^{2}/(2lsin\theta)^{2}=mgtan\theta ，所以 q=2lsinθmgtanθkq=\frac{2lsin\theta\sqrt{mgtan\theta}}{\sqrt{k}} 。

关于带电导体球的电容： C=qV=qkq/R=RkC=\frac{q}{V} =\frac{q}{kq/R}=\frac{R}{k} ，(R为导体球半径)

因而电势就是 V=qC=2lsinθmgtanθkRk=2lsinθkmgtanθRV=\frac{q}{C}=\frac{2lsin\theta\sqrt{mgtan\theta }k}{R\sqrt{k}}=\frac{2lsin\theta\sqrt{kmgtan\theta }}{R}

卡伐洛静电计电势与偏转半角的关系曲线

能看出来卡伐洛静电计，在偏转角不太大的时候，确实近似是曲线。

关于通草球静电计还有一种，就是亨雷象限静电计，介绍将鄙人面停止。

1.2. 伏打关于静电计的奉献

伏打利用摩擦起电机的转数和放电火花的数目丈量电量（卡文迪许评论摩擦起电机度量的问题，伏打后改用尺度化法式来度量电量和电势），曾利用卡伐洛静电计丈量电压。伏打已经发现了关于平行板电容器：电容与面积成反比，与间隔成反比[1]，而且极板感化力与电压平方成反比。

1786年，伏打和本纳特给静电计毗连了一个在末端点燃了的电极，伏打发现：火焰的电势与空气不异，那种火焰静电计在19世纪下半叶因为开尔文的倡议而得到普遍利用[2]；1787-1789年伏打将他的验电器的两个金属线换成了两根稻草，造做了稻草静电计[2]。那种静电计后来被英国电报之父弗朗西斯罗纳德用来丈量大气电。

在那不能不提到，伏打提出的同一电势丈量的纲领[3]：

i.利用统一种静电计对差别角度的电压丈量停止一种同一（尺度化法式 standardized procedure）；

伏打先找了一种基于静电感应，对电压和电量停止度量的好办法[3]：

a.关于1个平行板电容器，先把此中一个极板A毗连一个大容量的带电莱顿瓶。

b.断开莱顿瓶与A的连线，让另一个极板B接地，B因为静电感应会带上与A等量相反的电荷；

c.把B的接地线断开，让A与一个莱顿瓶毗连，在A与莱顿瓶的电传导与B对A的静电感应的配合感化下，A的电量和电势均会发作变革

（电量变成QCa/(Ca+Cp)，Ca和Cp是A和莱顿瓶的电容，从而AB电势差会减小到VCa/(Ca+Cp)；随后B接地，因为带上与A等量相反的电量，从而形成B的电荷绝对量也和A一样，以统一比例降低，形成电势差也降低统一比例）；

d.反复步调bc若干次。

按照理论阐发可知，两个极板的电量和电势是跟着次数指数衰减的。通过那种办法就能够对其它静电计停止有效定标。以上办法就是伏打度量电量和电压的Standardized Procedure，也就是尺度化法式，原理和本纳特的静电起电机是根本不异的。

伏打关于电势丈量的仪器

伏打发现他的稻草静电计至少在1到20度以内都能够包管与电压的线性关系，亨雷象限静电计在15度到35度[2]都能够包管与电压的线性关系[3]。

伏打稻草静电计，伏打曾经研究差别稻草静电计之间角度的关系的尝试

按照英国皇家科学促进会在1850年由Kew给出的陈述：伏打的稻草静电计与偏转半角的正弦成反比；亨雷象限静电计的读数的形式与伏打稻草静电计几乎一样，只是伏打的稻草静电计精度更高。[4]伏打稻草静电计的1度偏转相当于亨雷象限静电计的0.1度[5]，以至0.01度[4]。伏打稻草静电计后来被用于研究伏打电池，伏打发现一个锌银伏打电池的电压能够让稻草静电计偏转1/60度[5]。

Konochenhauer得到的关于稻草静电计的电量-角度关系曲线

Konochenhauer曾经通过莱顿瓶为稻草静电计停止定标，尝试发现静电计上的电荷与偏转角不是严酷的线性关系，斜率会跟着偏转角的增大而增大，通过Konochenhauer以下表格的数据就能看出来。再按照电压和偏转角的线性关系，能够发现稻草静电计跟着偏转的增大电容会变大。以下表格其实是Konochenhauer研究电介量束缚电荷库仑定律的尝试，通过差别间隔下束缚电荷关于静电计的感应电荷，能够看出场强的大小，通过以下数据能够看出静电计的感应电量与间隔平方成反比[6]（进一步表白束缚电荷与自在电荷性量的一致性）。

束缚电荷与静电计的间隔稻草静电计偏转角静电计电量130.68211.42.2536.20.95亨雷象限静电计，如图表盘分红了四个象限

ii.选择一种“根本度”(fundamental degree )来做为电压参考的一种单元[3]。

伏打曾经也研究过静电力的定量表达式，只不外伏打研究的是吸引圆盘之间的感化力：利用下面的吸引圆盘静电计，那种静电计是依靠杠杆平衡的原理：将静电力与砝码重力相平衡的办法。[3]

伏打吸引圆盘静电计

伏打 通过关于那个他的吸引圆盘静电计定义了电压尺度“根本度”：间隔2英寸的5英寸曲径极板之间的电力，当与12格令(6.3732g)的砝码平衡的时候的电压，定义为“根本度(fundamental degree)”。伏打发现此时亨雷静电计有35度的偏转角[3]。后来有了电压绝对丈量的办法以后（参考第4部门：绝对静电计），Giovanni Polvani和Giovanni Adorni 发现伏打的根本度“fundamental degree” 等于 44.5 个绝对静电单元, 也就是13,350 volts[3]。所以亨雷静电计，1度相当于大约400V；因而伏打稻草静电计的1度相当于40V[5]。一个锌银伏打电池的电压能够让稻草静电计偏转1/60度，所以是近似0.7V[5]。

别的关于中学利用的金箔静电计和本纳特金叶静电计的偏转角与电压的关系，也能够用卡文迪许和伏打的办法来验证与丈量。

不外，既然中学利用的Braun金箔静电计和本纳特金叶验电器偏转角与电压不是线性关系，那么为什么电学家会一而再、再而三用金箔静电计的偏转角间接来丈量电压呢（其时不叫electric pressure，而是electric tension电张力）？其实包罗卡伐洛静电计，按照以上推导可知，也不是严酷的线性关系。良多情况下，我们能够在必然的范畴内停止线性近似。

Braun Electrometer，Ferdinand Braun 于 1887年创造2.金叶验电器

然而固然都是金箔静电计，但是中学利用的和本纳特创造的在构造上存在必然差别，灵敏度也差别，因而线性区纷歧样，好比说中学的线性区小的几乎能够忽略。通过以上例子能够发现，良多静电计其实不完满是关于电压线性函数，但是在存在线性区：线性范畴能够通过我上面说的伏打和卡文迪许的尝试或者用平行板电容器来验证。

伏打电容验电器

我一再强调通过尝试的体例给金箔静电计定标，是因为在推导金箔静电计电压、电量与偏转角关系的时候，关于金属外壳和指针的电荷散布的推导有必然的复杂性，就算近似往往也不尽如人意。不外阐发仍是需要的：若是说叶片的长度是l，量量是m, 电容器的电容是C，电势差是V, 内层的电量为q, 重力加速度是g，偏转角为 ϕ\phi

给验电器加电势差，然后立马对静电计绝缘。随后叶片起头偏转的时候，到叶片静行的时候，对叶片重心列的重力势能的变革能够写为： mgl(1−cosϕ2)mgl(1-cos\frac{\phi}{2})

所以重力做功就是 Fcosθds=−12mglsinϕ2dϕFcos\theta ds=-\frac{1}{2}mglsin\frac{\phi}{2}d\phi

所以重力 |Fcosθds|=12mglsinϕ2dϕ\left| Fcos\theta ds \right|=\frac{1}{2}mglsin\frac{\phi}{2}d\phi

因为静电能的表达式是 E=12V2CE=\frac{1}{2}V^{2}C ，关于电能全微分：

dE=CVdV+12V2dCdE=CVdV+\frac{1}{2}V^2dC

按照q=CV，所以电荷转移全微分 dq=CdV+VdCdq=CdV+VdC

因而，电源透过电荷转移所做的功是， dW=Vdq=VCdV+V2dCdW=Vdq=VCdV+V^2dC

在系统到达不变的时候，动能为0，按照功用关系：CVdV+V2dC=CVdV+12V2dC+|Fcosθds|CVdV+V^2dC=CVdV+\frac{1}{2}V^2dC +\left| Fcos\theta ds \right|

因而重力克制静电力动弹叶片做的功就能够暗示为

|Fcosθds|=12V2dC=12mglsinϕ2dϕ\left| Fcos\theta ds \right|=\frac{1}{2}V ^{2}dC=\frac{1}{2}mglsin\frac{\phi}{2}d\phi

整理一下就酿成了 mglsinϕ2=V2dCdϕmglsin\frac{\phi}{2}=V ^{2}\frac{dC}{d\phi} ，

所以 V2=mglsinϕ2dCdϕV^2=\frac{mglsin\frac{\phi}{2}}{\frac{dC}{d\phi}}

若是我们把C关于偏转角 ϕ\phi 做泰勒展开，关于当 ϕ\phi 取值足够小的时候，电容C的高阶项能够忽略，能够看做 dCdϕ\frac{dC}{d\phi} 能够看成一个常数，此时 sinϕ2≈ϕ2sin\frac{\phi}{2}\approx\frac{{\phi}}{2} ，所以电压的平方与验电器的偏转角近似成反比。从那个角度上来说，若是太小的角度其实不能做线性近似。

“金箔静电计在偏转角很小很小的时候，按照泰勒级数展开，能够忽略高阶项，能够只保留线性重量”那个说法其实是错的（固然我以前那么认为）。

但是稍大一点的偏转角呢？

其实那种构造的静电计，定量推导是很困难的，尤其我们很难推导它的电容公式，不外能够接纳尝试的办法为静电计定标。下面做一下介绍，

3.半定量电压定标的办法 3.1. 电容定标法

关于为静电计定标就能够基于两种半定量丈量电压的法子：

1. 电容并联法：在电量连结稳定的情况下，把不异的电容并联，就能够让电容倍增，电势差减半，如许以来就能够操纵电容和电势差成反比的关系来半定量丈量电压（就像卡文迪许的法子）；

2. 电容定义法：也能够连结电容（几何构造还有质料品种确定的导体，按照静电场独一性定理，电容连结稳定）稳定，丈量电量，按照电量与电压成反比的办法来半定量度量电压。如图所示静电计中有一个半径很大的铜球，能够通过丈量它的电荷来度量它的电势（导体球有一个益处：因为晓得电荷仅仅散布在外表，且面密度平均，那么就算不消静电场独一性定理，也能推出电量与电势的反比关系）。帕尔贴(Peltier)曾经通过库仑扭秤为帕尔贴磁针静电计（操纵电力与磁力相平衡的办法）定标；帕尔贴静电计，帕尔贴创造于1830年代Quetelet曾经利用两个半径不异的小球接触，电荷平分的办法半定量度量电量（那也是伏打的一种办法）。他用两个静电计的小球接触来平分电荷；此中一个静电计放电，与另一个静电计接触再次平分获得一起头1/4的电量。他对帕尔贴静电计给出如下成果[7]

：电量库仑扭秤偏转帕尔贴静电计偏转12825度74.5度1/21400度70度1/4795度64度毕奥就曾接纳扭秤丈量电量的那种法子（关于丈量电量的法子能够基于库仑扭秤和汤姆逊象限静电计，关于丈量电量几种路子的辨析以及起电机的原理，我在那里面曾经答复过）。 电量用两个半径不异的小球接触电荷平分也是不异的事理，

伏打已经发现了关于平行板电容器：电容与面积成反比，与间隔成反比。[1]3. 平行板电容器定标法：因为平行板电容器的电容公式是 C=\varepsilon_{0} S/d=Q/U

，能够在电量连结稳定的情况下，按照U与d成反比（那个关系之前也被（伏打）伏打用卡伐洛静电计尝试来验证）来对电压停止半定量丈量。但是边沿效应是难以回避的问题。

通过那些办法能够实现对静电计的有效定标。但是那些办法也有局限性，好比说精度有限。因而需要寻找更有效的定标路子，

伏打电池的创造为我们指了然标的目的，伏打察看到了那种电池能够让静电计发作偏转。1802年，德国物理学家马隆(M. van Marum)和普法夫(C. H. Pfaff)曾用电池给莱顿瓶充电，那与摩擦起电机的特征类似。与此同里特(J. W. Ritter)也证了然电池的电极之间能够产生吸引和排挤现象。那些现象表白伏打电池也具有和摩擦产生的电类似的性量。通过进一步的研究，我们发现，化学电池能够用做静电计定标的手段。

4.那也就是”串联电池电势差定标法“：因为电势差反比于串联的尺度丹聂耳电池的数量（伏打电池和伏特电池也行，因为是断路形态下丈量电势差，因而无电流，也就不存在电池极化了）。但是那种办法需要基于两个尝试成果：i. 构造确定的电池的断路电压是确定的（至少在电池刚出厂）；ii. 两个构造确定的电池串联，电压等于两个电池电压的和。科尔劳施曾经建议利用伏打电池来对摩擦电停止度量，而且提出用那种办法做为比力差别的静电计的办法[6]。

3.2. 伽伐尼电池定标

下面介绍一下若何得出以上两个尝试成果：

第一个尝试成果：能够确定"构造不异的电池电压不异"，只要用"晓得定性关系的"静电计就能够确定了，好比“关于构造不异的电池，静电计的偏转角一样或者偏转角稳定来确定电池电压不异”；不外伏打电池和丹聂耳电池电压很小，只能通过将十几个到几百个电池串联，构成一个新的大电池（大电池的构造不异，不只是小电池的构造要不异，小电池串联的数目也要不异）；按照串联数量的差别能够操纵稻草静电计来确定大电池的电势差在构造不异时的相等关系，再不济能够利用上面介绍的第一种半定量丈量电压的办法：用电量来度量电势差。

第二个尝试成果：证明电势差的可加性，也需要利用适才说的大电池：我们需要先丈量两个大电池的电势差；然后再把那两个大电池串联，丈量它们的总电势差。那个尝试需要实现关于电势差的半定量丈量，能够基于上面介绍的两种半定量尝试的办法，也能够利用通过以上两种半定量尝试定标的静电计来验证。

下面介绍一下伏打用电容静电计来验证电压与电池串联数目标关系的尝试：当伏打把1个伏打电池接入稻草静电计时，发现静电计偏转角为3度；当伏打把2个伏打电池接入静电计时，发现静电计偏转角为6度；当伏打把3个伏打电池接入静电计时，发现静电计偏转角为9度；当伏打把4个伏打电池接入静电计时，发现静电计偏转角为12度[8] [9]

.在1.2部门，我们已经介绍了稻草静电计的偏转角和电压是成反比的。

结论：很明显，伏打的尝试必定了，电压和串联电池数量是成反比的！！！

问题：不外那容易有个疑问，那就是固然此时验电器的精度到达了18世纪更高的水平，而且能够通过增大毗连在静电计上的电容器的极板间隔来增大静电计的偏转角(能够将偏转角度放大120倍)，但伏打电池的电势差很小，很可能减小与其毗连的平行板电容器的电容也无济于事。本纳特很早之前就考虑到了那个问题，因而提出了一种静电感应的倍增法，但是那种电倍增器摩擦太大很难推广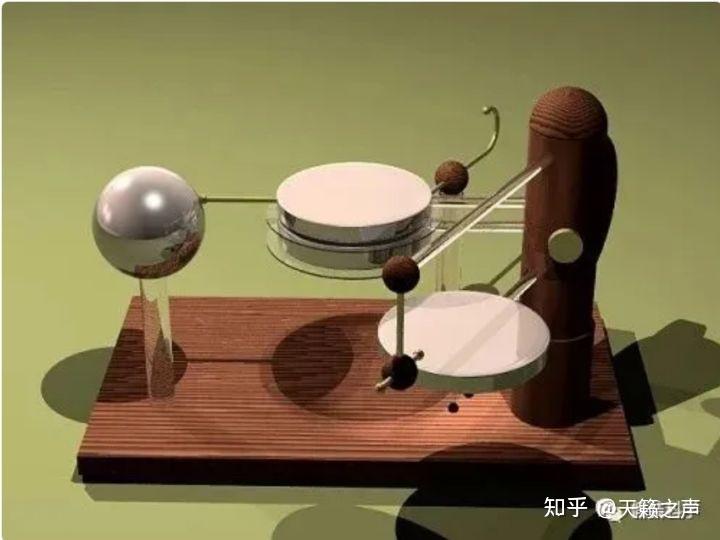，尼克尔逊动弹倍增器后来尼克尔逊改良了本纳特的倍增器，创造了尼克尔逊动弹倍增器（原理与本纳特倍增器差不多，能够参考下面阿谁链接里第三部门的内容）。[10]伏打就是利用了那种动弹倍增器，将伏打电池的极板电量与电势差倍增到了通俗静电计能够丈量的水平[11]。3.4. 对金箔验电器的精细定标 随后Andreissen改良了金叶验电器，在玻璃瓶内加拆桶状的抛光的黄铜导线，如图中的abide，那种静电计在不利用电容器的情况下，也能够完成伏打做的那些根本的尝试[6]。随后法拉第在静电计的内外表加拆了一层金属层[12]，使得金箔静电计愈发靠近今天的形式。Andriessen改良的金叶静电计

不管怎么说，我们最末找到了第三种电压半定量定标的办法：串联电池电势差定标法

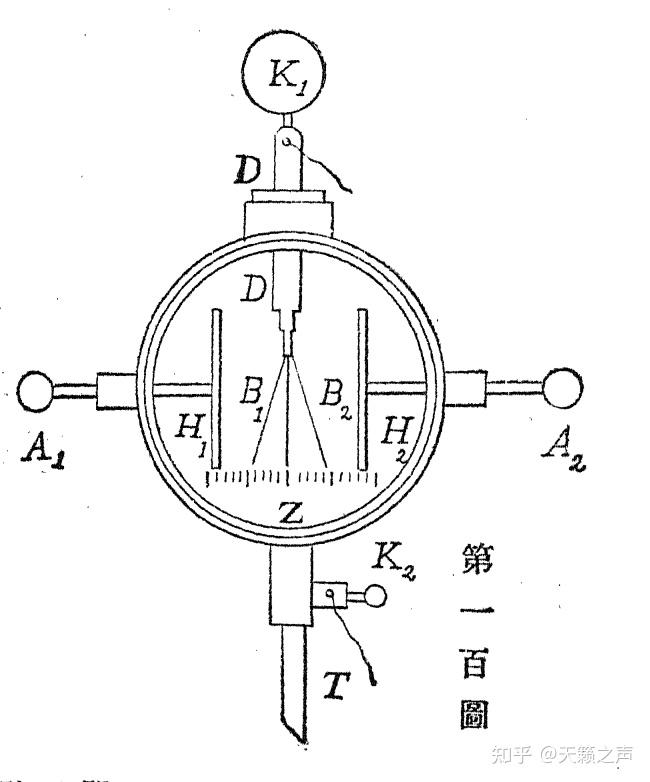Exner 静电计

通过以上所说的办法就能够实现对金箔验电器停止愈加精细的定标，FR. Kolacek. 曾经在1886年的魏德曼物理年鉴上给出了他的尝试过程。他研究了叶片长8厘米的金箔验电器[13]。通过毗连差别数量的丹聂耳电池，在光谱千里镜和螺旋测微计读出静电计差别的程度偏转位移[13]（叶片张开间隔，参考上面的Exner 静电计的程度刻度），我们晓得金箔验电器原来精度其实不高，但是共同那些细密的光学仪器即是如虎添翼。尝试关系如下，电池数量n与程度位移x的关系

n=\sqrt{3.825x+3.032x^{2}} ，那个成果在小于18度的情况下，差不多在叶片间隔小于2.5cm的情况下能够成立

因为电池数量与电压V成反比：V=kn，所以 V=k\sqrt{3.825x+3.032x^{2}} [13]

接下来，Kolacek 通过尝试丈量了比例系数k，为了进一步包管精度，他必需包管电池在断路形态下电流很小，因为若是电池有电流，路段电压将会比理论值小，从而不再与个数成反比。他用镜式电流计给出的成果是电流小于万万分之一安培[13]。要想丈量比例系数k，必需实现对电压的绝对丈量才行，不外上面仅仅提到了相对丈量，没有说绝对丈量。关于绝对丈量的办法请参考第4部门“汤姆逊绝对静电计”。

Kolacek通过利用已知绝对电压的144个串联的Beetz干电池丈量验电器的程度位移，最末比例系数：k=240.0

金箔验电器：电压-程度位移曲线，程度位移每个格2.65厘米，电压为每个格250V

能够看出在2.5厘米以内，在很大的范畴里都很接近曲线，只要在比力小的区域V(x)才接近第二部门里说的无理函数。

3.5. 细小电位的探测

静电计的定量丈量绕不开的话题，就是若何进步静电计的精度，也就是检测细小电位的才能。其其实上一栏目我们已经介绍了一些细小电位检测的办法，但是要提一下1814年由德国物理学家Bohnenberger所创造的——Bohnenberger静电计，那种仪器最后的创造者其实是T.G.B. Behrens[14]。那种静电计把上千个伏打电池串联，正负极毗连在静电计玻璃罩侧面的金属薄片上，如许会在静电计的程度标的目的产生很大的电势差，接下来把待测物体毗连到指针上面，只要侧面金属薄片上的电势差足够大，即使待测物体电位很小，也会有明显偏转。后来Bohnenberger为了进步精度，把伏打电池换成了干电池。所以那种静电计又称干电池静电计，那种静电计没有像本纳特金箔验电器那样接纳裤衩型的指针，而是把双箔片换成了单箔片——如许静电计就能检测待测物体是正电势仍是负电势。

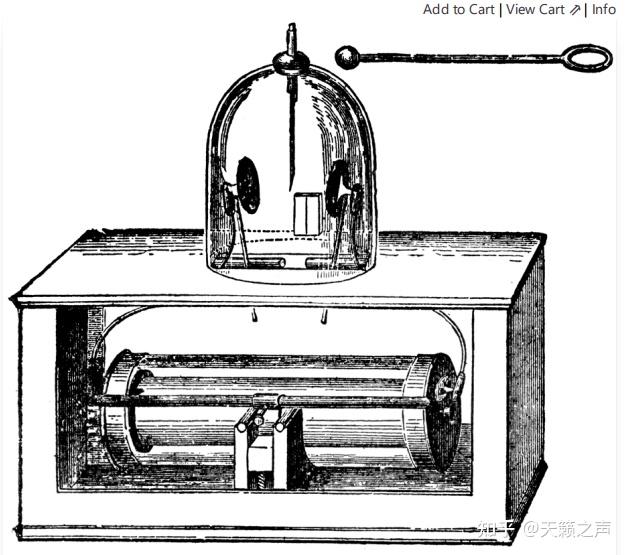Bohnenberger干电池静电计

Wilhelm Gottlieb Hankel后来改良了干电池静电计，那小我是数学家汉克尔的父亲，教师是改良电流计的施威格。那就是汉克尔细丝静电计，汉克尔把薄片换成只要1-2毫米铂丝，那种静电计有比力小的自电容和很高的灵敏度，与显微镜共同利用[15]。同时他利用一个包罗大量干电池单位的伽伐尼电池，而且包管与电池毗连的两个极板产生很慢的挪动，而且加拆了刻度。[16]那种静电计能够到达1-100V的丈量范畴。

Hankel Filament Electrometer

那种静电计启发了后来的汤姆逊象限静电计，后面会做介绍。

还有就是一般静电计会力图在初始形态静电计的偏转是0，为了消弭零点误差，奥斯特接纳了磁针式的扭称静电计[6]，后来帕尔贴的构造也类似。

4.绝对静电计 4.1.哈里斯吸引圆盘静电计

我们已经找到了3种半定量丈量电势差的办法，那么若何实现对电势差的绝对度量呢？上面提到的卡伐洛通草球静电计就能够。别的，我们晓得第二种半定量丈量办法”平行板电容器法“，就能够实现绝对丈量，哈里斯爵士改良的吸引圆盘静电计就是操纵那个原理。很明显，他的静电计是对伏打圆盘静电计的改良。

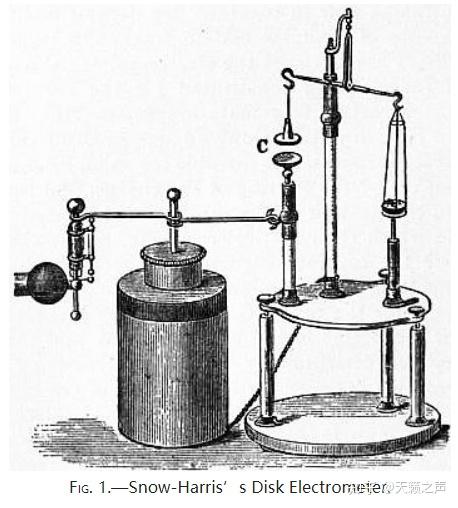
那素质就是一种静电天平：电力与砝码重力的杠杆平衡。

若x是极板间隔，V是电势差

电容器的一个极板的电场强度是： E=\frac{V}{2d} ,

极板的彼此感化力是 F=\frac{VQ}{2d} ，Q=VC

因而 Q=VC=\frac{V\epsilon_{r}S}{4\pi kd} ，静电力就是 F=\frac{V}{2d}·\frac{V\epsilon_{r}S}{4\pi kd}=\frac{V^2\epsilon_{r}S}{8\pi kd^2}

所以电势差就是： V =d\sqrt{\frac{8\pi kF}{\epsilon_{r}S }}

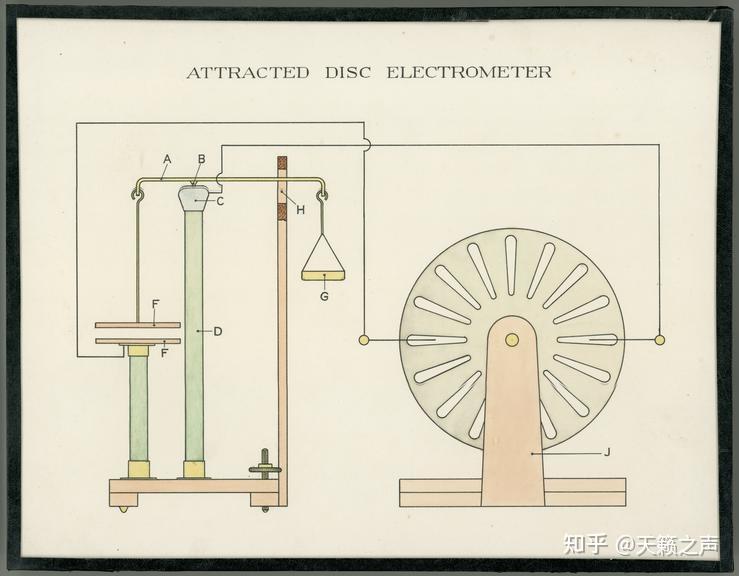吸引圆盘静电计（电压天平）

关于等臂杠杆，因为杠杆平衡，所以F=mg, mg为砝码重量

V =d\sqrt{\frac{8\pi kmg}{\epsilon_{r}S }}

后来开尔文对那种静电计停止了改良，为了消弭边沿效应加拆了庇护环，那就是开尔文天平。时至现代，开尔文天平不断还做为电压绝对丈量的仪器。在20世纪的不竭改良傍边，间隔d能够接纳激光干预仪来丈量，电容可改用交换电桥法来丈量。目前国际上用此法停止电压绝对丈量的有德国联邦物理手艺研究院PTB和南斯拉夫萨格勒布大学，不确定度别离为2.74×10^-7(1992年)和2×10^-7(1994年)。

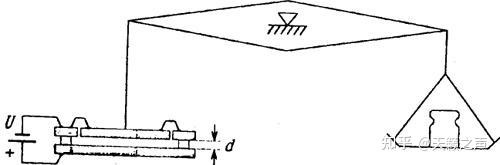那种静电计在圆盘外侧加拆了庇护环，目标是消弭边沿效应

接下来我要介绍的另一种绝对静电计——汤姆逊绝对静电计，那是对哈里斯爵士静电计的改良,开尔文加拆了庇护环。庇护环与平行板在统一个平面上，但是连结了必然的间隔，是因为需要制止接触的时候产生电火花。

那一部门将大量应用平行板电容器电容的公式，但是那个公式是一个近似的形式，关于圆盘电容公式的进一步研究请参考下面那篇文章中的第3部门

4.2.汤姆逊绝对静电计 汤姆逊绝对静电计，汤姆逊于1855年创造

下面我们对静电计做一下理论阐发，咱们用一种差别的阐发体例：接纳功用关系的阐发。我们假设静电力是F，在两个圆盘之间加了恒定电势差V，圆盘电容器电容是C、间隔是x。我们晓得因为圆盘之间存在吸引感化，所以x会发作变革，进而影响电容。按照静电理论，可知：电场力做功对应静电能的变革。设F为机械力（是与电力平衡的弹簧弹力），因为大约有一半的静电能会酿成机械势能。

电场能变革对应， dE=\frac{1}{2}(C+dC)(V+dV)^{2}-\frac{1}{2}CV^{2}=\frac{1}{2}(C+dC)(V^2+dV^2+2VdV) =\frac{1}{2}(CV^2+CdV^2+2CVdV+dCV^2+dCdV^2+2dCVdV)-\frac{1}{2}CV^{2}

=\frac{1}{2}(CdV^2+2CVdV+dCV^2+dCdV^2+2dCVdV)

舍去高阶无限小，能够得到全微分：

dE=\frac{1}{2}(2CVdV+V^2dC)=CVdV+\frac{1}{2}V^2dC

按照电荷转移全微分 dq=CdV+VdC

因而，电源透过电荷转移所做的功是， dW=Vdq=VCdV+V^2dC

在系统到达不变的时候，动能为0，按照功用关系：CVdV+V^2dC=CVdV+\frac{1}{2}V^2dC +Fdx

因而弹力克制静电力、挪动带电体做的功就能够暗示为

Fdx=\frac{1}{2}V ^{2}dC

整理一下就酿成了 F=\frac{1}{2}V ^{2}\frac{dC}{dx} ，

又因电容器一对圆盘是平行板电容器，为了削减边沿效应，因而如下图加拆庇护环(Guard Ring)，因而电容能够表达为： C =\frac{\varepsilon_{0} S}{x} (farads)，因而 \frac{dC}{dx} =-\frac{\varepsilon_{0} S}{x^{2} } ,代入上面的等式，就能够得到力的绝对值 F=\frac{1}{2}V ^{2}(\frac{\varepsilon_{0} S}{x^{2} })=\frac{1}{2}V ^{2}(\frac{\varepsilon_{0} S}{x^{2} })

整理一下就酿成了： V ^{2}=2F(\frac{x^{2}}{\varepsilon_{0} S })

开平方就是 V =x\sqrt{\frac{2F}{\varepsilon_{0} S }} volts， 从而也就实现了对电压的绝对丈量

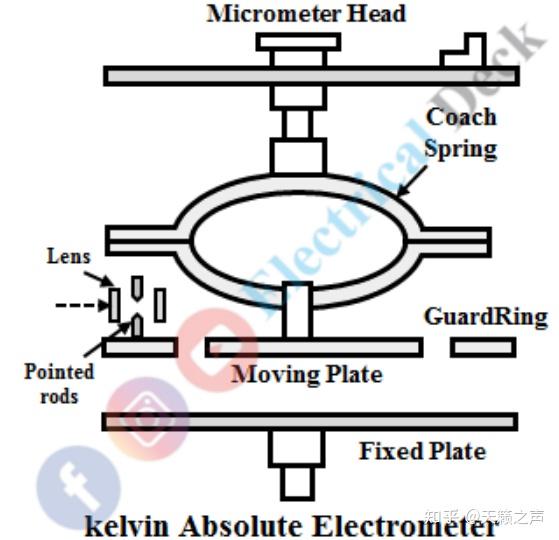汤姆逊绝对静电计构造图

需要指出那种静电计只能用于高电压的绝对丈量，不外那却足以把绝对丈量再往前推一步：前面刚刚提到一种半定量丈量办法——串联电池电势差定标法，那是基于”在不异构造的电池串联时，电压于电池数量成反比“。若是我们把上千个电池串联的话，在把它们的正负极毗连到静电计的两个圆盘上，就能够操纵上面的法子对他们停止电势差的绝对丈量。测出电池组的电压后，再除以电池组串联的尺度电池的数量，就能够定出尺度电池的电势差。

能够通过光的反射来读出弹簧的位移

威廉·汤姆逊先后利用两种办法丈量了丹聂耳电池的电动势：1851年是通过焦耳定律[17]，丈量了在cgs电动力学单元造下的电动势，为 10^{8} 个cgs电磁单元；1860年又通过静电的办法丈量了扭称静电计偏转角与绝对静电计圆盘感化力和电势差的关系，最末通过那两种静电计研究了丹聂耳电池的电动势的绝对静电丈量（开尔文一下丈量了284个串联的电池）[18]，汤姆逊通过绝对圆盘静电计测定丹聂耳电池的静电电压是0.00374个cgs静电单元，对应 1.121\times10^8 个cgs电磁单元（按照韦伯测定的电磁单元电量与静电单元造的电量的关系——光速），即1.121V[19]。1861年，布莱特（Bright）和克拉克（Clark）提出的电压适用单元就与丹尼尔电池不异，称做欧玛德(ohmad)，后被英国电学单元委员会改为伏特（Volt），后来成为法国、德国的尺度。1873年，逐步接纳伏特那个单元，在那之前多接纳丹尼尔或罗甫电池的电动势之比来暗示电压。如今，尺度丹聂耳电池的电势差在25摄氏度下，大约是1.1V。

如许一来，”串联电池半定量电势差定标法“就酿成了”串联电池绝对电势差定标法“，我们就找到了另一种电压绝对丈量的法子”串联电池绝对电势差定标法“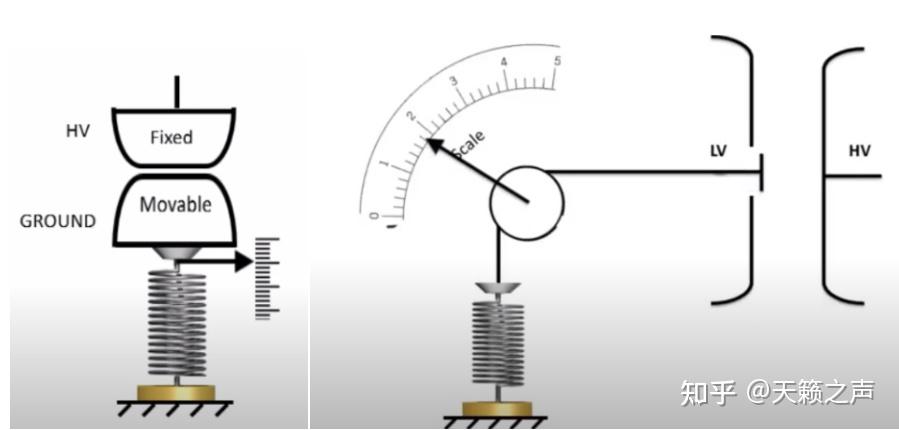绝对静电计革新的电压表

通过给弹簧或者给滑轮加拆指针，就能够把那种静电计做成间接读数的静电电压表。

5.汤姆逊静电电压表

固然那玩意叫电压表，但是那个原理是蝴蝶外形的平行板电容器的电势差形成带电的领结型薄片偏转，从而带动指针的偏转，所以那素质上是基于静电原理的。那种通过汤姆逊绝对静电计或者串联电池绝对电势差定标法能够完成对汤姆逊静电电压表对应的伏特数停止标定，那也就是为什么它要叫电压表(Voltmeter)了。那种电压表曾经做为英国适用电压单元复现的尺度。

汤姆逊静电电压表

能够看出电压和偏转角并非线性的关系，偏转角越大灵敏度越低，而且那种静电计合适丈量50V-10000V的电压[20]。之所以会改变，是因为两个极板（指针极板和固定极板）并非完全正对的，所以电场线不是垂曲于极板的，而是倾斜的，恰是倾斜的电力带动指针极板改变。以前喜好利用重力平衡，但后来多利用弹簧平衡[21]。那种原理与接下来要讨论的象限静电计千篇一律，所以推导间接参考象限静电计就行。

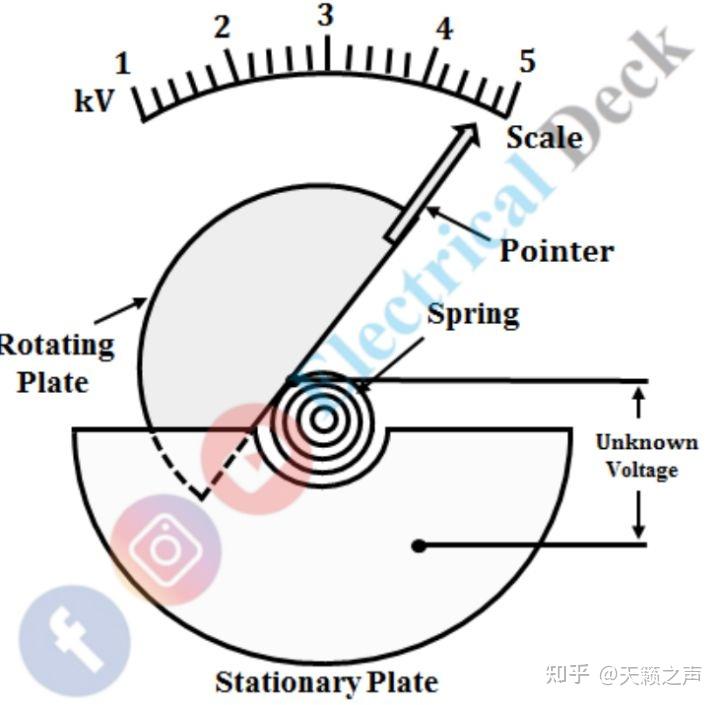汤姆逊静电电压表表盘6. 汤姆逊象限静电计

1867年，威廉·汤姆逊创造了汤姆逊象限静电计。下面我对汤姆逊象限静电计的构造做一下简要介绍，并介绍丈量电压的办法——也就是做一下关于静电计偏转角与电压关系的数学推导。

汤姆逊象限静电计6.1.理论阐发与推导

如下图所示，那种静电计的指针是蝴蝶外形的，有一根悬丝S将其垂曲悬挂，下方有四个1/4扇形的电极。若下面左图所示，扇形电极把平面分红4个象限，如右图所示，一三象限电极BB用导线毗连，二四象限电极AA用导线导通，但是AA与BB连结绝缘的形态。从而AA是一个蝴蝶形的等势体，BB也是一个蝴蝶外形的等势体。把待测电势差的导体的正电位与AA相连，负电位与BB相连，同时让指针处于正电位。如许以来因为BB负电荷与指针正电荷吸引，AA的正电荷与B的正电荷排挤，所以会形成领结型指针靠近BB而远离AA，也就是形成指针顺时针改变，我们设改变角为θ。

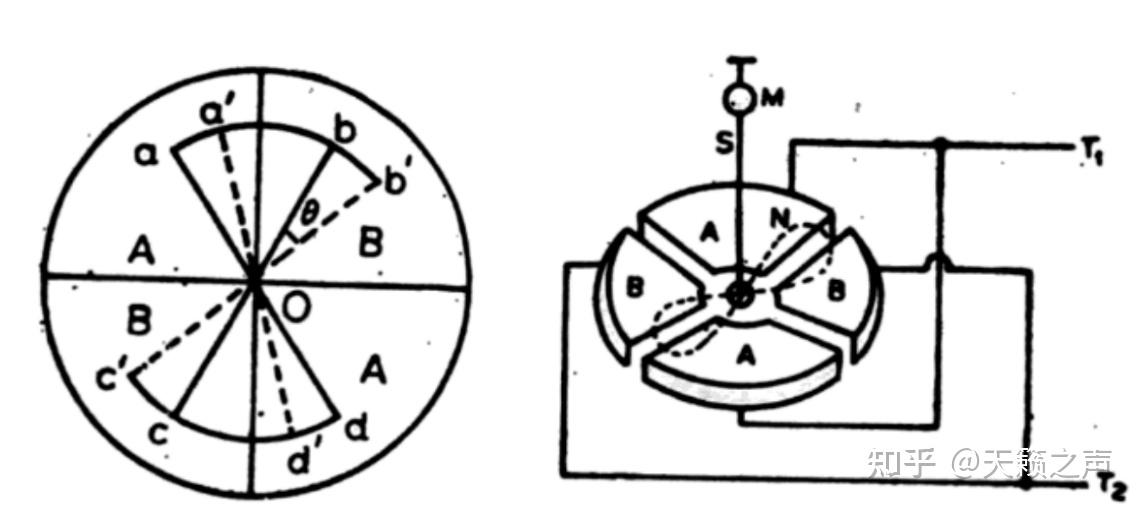汤姆逊象限静电计电极与指针示企图

此外那个系统能够看成是指针与BB构成的电容C1与指针与AA构成的电容C2的并联，能够看出那两个电容都是平行板电容器，因而电容公式式 C =\frac{\varepsilon_{0} S}{x} ；C1电容公式中的面积就是指针与BB的相对面积，C2电容公式中的面积就是指针与AAB的相对面积。

我们晓得圆心角是θ的扇形的面积就是 \frac{1}{2}r^{2}\theta ，又因为指针是由两个中心对称扇形所构成的蝴蝶外形，因而在指针动弹θ角的情况下，C1电容器的正对面积变革量和C1电容器的正对面积的变革量绝对值就满足 \Delta S=2·\frac{1}{2}r^{2}\theta=r^{2}\theta ，只不外指针与BB的正对面积增加那么多，与AA的正对面积削减那么多。因而指针与BB之间的电容增大，静电能升高；指针与AA之间的电容减小，静电能降低。电容总变革量绝对值就等于 \Delta C =\frac{\varepsilon_{0} \Delta S}{x} =\frac{\varepsilon_{0} r^{2}\theta}{x} 。

若是我们设指针、BB、AA的电势别离为Vo、Va、Vb，因而指针与BB的电势差是Vo-Vb，指针与AA的电势差是Vo-Va。那么我们就能够计算并联的那两个电容器的静电力做功的绝对值。

因而我们能够晓得，在指针偏转指针与BB构成电容器的静电能增量绝对值是 \Delta E_{b}=\frac{1}{2}\int_{C_{1}}^{C_{1}+\Delta C}UdQ=\frac{1}{2}\int_{C_{1}}^{C_{1}+\Delta C}U^2dC ;

因为电势是确定的，因而电势差也是确定的，从而U^2就能够从积分号中被提出来 \Delta E_{b}=\frac{1}{2}U^2\int_{C_{1}}^{C_{1}+\Delta C}dC=\frac{1}{2}U^2\Delta C=\frac{1}{2}\Delta C(V_{o}-V_{b})^{2}

因而我们同理也能够晓得，在指针偏转指针与AA构成电容器的静电能增量的绝对值是 \Delta E_{a}=\frac{1}{2}\Delta C(V_{o}-V_{a})^{2} ;

又因为指针与BB之间，静电力做正功；指针与AA之间静电力做负功；因而静电能增量绝对值就是 \Delta E_{静}=\Delta E_{b}-\Delta E_{a}=\frac{1}{2}\Delta C(V_{o}-V_{a})^{2}-\frac{1}{2}\Delta C(V_{o}-V_{b})^{2} ;

化简就得到 \Delta E_{静}=\frac{1}{2}\Delta C[(V_{o}-V_{a})-(V_{o}-V_{b})][(V_{o}-V_{a})+(V_{o}-V_{b})]

再进一步化简最末就得到， \Delta E_{静}=\frac{1}{2}\Delta C(V_{b}-V_{a})[2V_{o}-(V_{b}+V_{a})]

把电容变革绝对值带进公式，就得到了 \Delta E_{静}=\frac{\varepsilon_{0} r^{2}\theta}{x}(V_{b}-V_{a})(V_{o}-\frac{V_{b}+V_{a}}{2})

因为关于指针，只要静电力和弹力做功，所以静电能与弹性势能加动能总和守恒，但是因为指针最末会静行下来，所以在指针不变的时候，动能为零，定义 \Delta E_{弹} 为弹性势能增量的绝对值，那也就意味着在不变或者迟缓挪动的时候 \Delta E_{静}=\Delta E_{弹}

接下来推导 W_{弹} 的表达式

我们假设弹性恢复力矩是M，我们晓得按照库仑在1784年按照尝试得到的扭秤扭力矩绝对值的公式是：

M=\frac{\mu D^{4}\vartheta}{L} , μ是悬丝弹性系数，D是悬丝曲径， \vartheta 是改变角，L是悬丝长度。

因为在那个尝试里弹性系数、曲径、长度均是定值，所以我们把上述公式写成 M=k\vartheta，此中 k=\frac{\mu D^{4}}{L} 是一个与悬丝相关的常数。我们晓得弹性势能变革绝对值就等于扭力矩做的功，即：

\Delta E_{弹}=\int_{0}^{\theta}Md\vartheta=\int_{0}^{\theta}k\vartheta d\vartheta=\frac{1}{2}k\theta^{2}

按照 \Delta E_{静}=\Delta E_{弹}

能够得到 \frac{1}{2}k\theta^{2}=\frac{\varepsilon_{0} r^{2}\theta}{x}(V_{b}-V_{a})(V_{o}-\frac{V_{b}+V_{a}}{2})

最末整理一下，就酿成了 \theta=\frac{2\varepsilon_{0} r^{2}}{kx}(V_{b}-V_{a})(V_{o}-\frac{V_{b}+V_{a}}{2})

1.在Vb、Va远小于Vo的时候， \frac{V_{b}+V_{a}}{2} 就能够忽略，公式能够近似为：

\theta=\frac{2\varepsilon_{0} r^{2}}{kx}(V_{b}-V_{a})(V_{o}-\frac{V_{b}+V_{a}}{2})\approx\frac{\varepsilon_{0} r^{2}}{kx}(V_{b}-V_{a})V_{o}

很明显此刻，静电计偏转角与电压成反比！

2.在Vb增大到与Vo相等的量级时，让Vo=Vb的时候，公式能够变更为：

\theta=\frac{2\varepsilon_{0} r^{2}}{kx}(V_{b}-V_{a})(V_{b}-\frac{V_{b}+V_{a}}{2})=\frac{\varepsilon_{0} r^{2}}{kx}(V_{b}-V_{a})({V_{b}-V_{a}})=\frac{\varepsilon_{0} r^{2}}{kx}(V_{b}-V_{a})^2

很明显此刻，静电计偏转角相对电压是二次函数的关系！

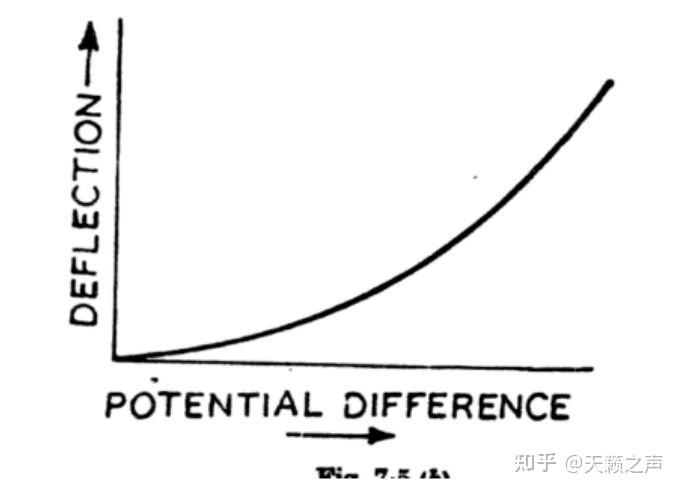Vo=Vb时，静电计偏转角与电压的二次幂函数关系6.2.尝试查验

接下来，我们用尝试的体例查验一下上面推导的公式，

电压不太大的情况下，能够用串联电池电势差定标法定标；在电势差过大的情况下，定标既能够利用串联电池电势差定标法，也能够利用汤姆逊绝对静电计或者汤姆逊静电电压表来定标。

针对汤姆逊象限静电计的定标，霍普金斯传授曾经利用串联电池电势差定标法，把18个丹聂耳单位为一组，构成一个大电池，通过电压与串联大电池数目成反比的办法丈量了电压与偏转角的关系：发如今偏转角不太大的情况下，偏转角与电压是线性的关系，

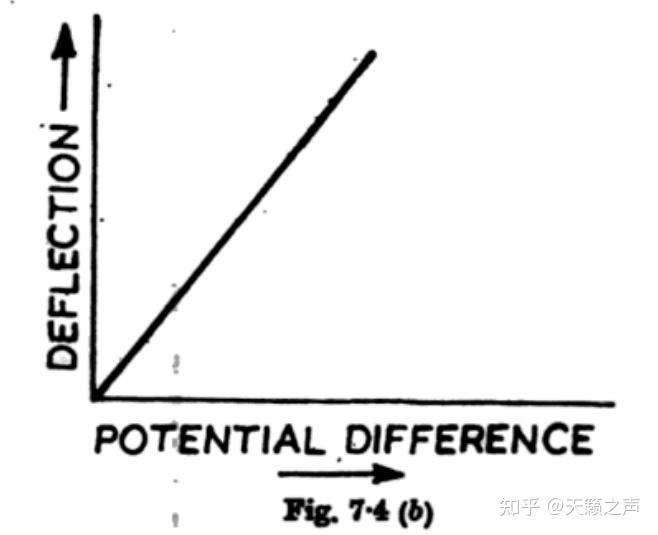小偏转角的函数图像

若是电极BB电势较大的情况下，偏转角比力大的情况下，偏转角与电压的关系能够满足上面推导的复杂函数 \theta=\frac{2\varepsilon_{0} r^{2}}{kx}(V_{a}-V_{b})(V_{o}-\frac{V_{b}+V_{a}}{2})

为了让静电计容易发作偏转，一般要让静电计指针的电势大一些。但是霍普金斯传授发现，上面那个偏转与电压的函数关系只在指针的电势在200V以下才成立，指针电势大于200V就跟理论值相差很远了，以至偏转角先随电压增加而增加、后随电压增加而减小[22]。为领会决那个问题，1886年-1889年，Ayrton、Perry 和 Sumpner放弃了汤姆逊象限静电计的象限电极的双丝悬挂构造，而改用单丝的磁控造构造，改良了汤姆逊象限静电计，最末尝试发如今指针电势高达3.6kV的情况下仍然契合理论成果，而且能够间接检测出1.4V以下的电势差（要实现比力好的精度，指针叶片的电势需要360伏以上），而且灵敏度比汤姆逊象限静电计更高。因而，只要有了汤姆逊象限静电计，曲流电压的静电计丈量就不在话下了（老觉得静电计不克不及测曲流电压，那是没有用那种高精度的静电计）。改良后的象限静电计指针末端有导线，导线插入到浓硫酸傍边 (浓硫酸有比力好的吸水性，从而包管比力好的绝缘特征)。

改良后的汤姆逊象限静电计

以上三种开尔文静电计的介绍除了参考开尔文的教材之外，也能够参考苏联的大百科全书以及不列颠在线百科。也能够参考一些国内的教材：好比民国1927年周毓萃的电磁学教程(由商务印书馆出书)[23]

6.3. 应用与改良

汤姆逊象限静电计比拟以前的所有静电计，具有更高的精度，麦克斯韦在1870年代利用汤姆逊象限静电计将库仑定律的精度提拔约3个数量级；19世纪末，汤姆逊象限静电计在大气电丈量中有普遍的应用，法国和德国的物理学家把它与复写笔、拍照底片毗连在一路，实现了通过了复写法、拍照法对大气电的实时记录。20世纪初，汤姆逊象限静电计实现了与电磁铁的毗连，能够愈加有效的记录大气电的变革。后来，汤姆生在丈量阴极射线粒子比荷的时候，在第一次尝试中也曾用到汤姆逊象限静电计（我们课本中说的是他设想的第二次尝试）；

皮埃尔·居里所建造的象限静电计

卢瑟福在研究α粒子的时候，曾用汤姆逊象限静电计和法拉第圆筒丈量单元时间射入静电计的总电量，而且在通过闪灼计数器测得单元时间通过的的α粒子数的情况下，得到了单个α粒子的电量，为两个单元元电荷；而且卢瑟福通过象限静电计丈量了元素的半衰期；居里夫人在研究元素放射性的时候，曾操纵汤姆逊象限静电计丈量辐射电粒子流密度。

Dolezalek和能斯特(Dolezalek是能斯特在哥廷根的学生和同事)改良了象限静电计，能够看到做的比汤姆逊象限静电计更精致了，外壳以至是象限电极都是用不锈钢做的。叶片做的更小，而且嵌入在象限象限电极里面，想翻开必需有专业的拆配手艺，灵敏度从0.1V进步到了0.01V，以至是5mV。（严酷来说，卢瑟福用的是那种象限静电计）

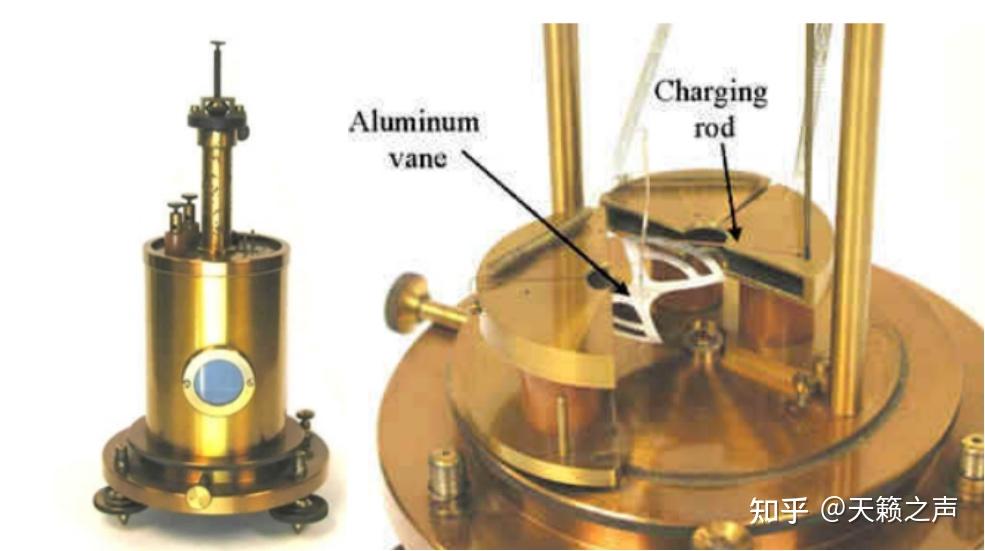1896年，由Friedrich Dolezalek设想的，Dolezalek静电计

至于Frederick Lindemann，将叶片从铝材换成石英纤维，接纳显微镜察看，因而大幅度提拔精度。20世纪20、30年代的光度学丈量，当科学家们难以提拔光电池和磁电式电流计的灵敏度时，转而考虑利用林德曼静电计，随后发现了林德曼静电计有良多电流计不具备的优势[24]。林德曼静电计从而被用于光度学的光电丈量——那种静电计在二战中还被被用于红外探测。不外随后在实空管放大器快速开展的时候，光度丈量便又回归了电流计。

Lindeman静电计(1924)

那些机械静电计的精度还能够更高，后来分辩率又提拔到了1mV，Kleiner象限静电计的更高灵敏度以至到达了1μV/mm，而且静电计的电容也做的越来越小。但是因为构造和操做上过于复杂，因而在现实应用中，已经根本不再利用，取而代之的是高阻抗的电子电压表和晶体管电子静电计。

注：德国的鲁道夫·科尔劳施利用德尔曼静电计在1848年研究了电路定律，得到了：“在导线的质料、横截面积和电流强度确按时，电压与导线长度成反比。”根据那个原理能够按照电压与电阻丝长度的关系，通过电阻丝对电池的分压能够对静电计停止愈加精细的定标。

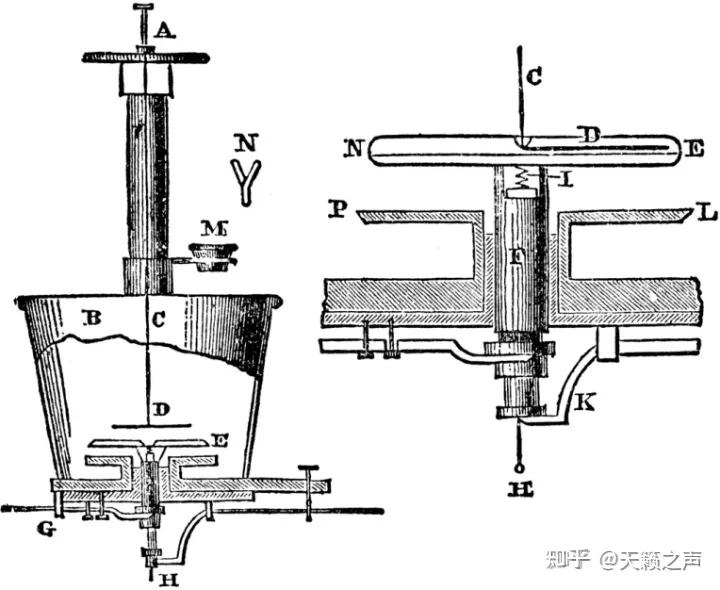德尔曼静电计，一种扭秤静电计，科尔劳施将德尔曼验电器改为德尔曼静电计。那种静电计构造比力复杂，不太便利停止理论推导，不外能够通过科尔劳施所倡导的加伐尼电池串联的办法停止精细定标7.布劳恩静电计最初再回到一起头说的中学经常利用的布劳恩(Braun)静电计，那种静电计是Braun与1887年设想的一种金箔静电计，能够说是以上的静电计中呈现比力晚的，比汤姆逊象限静电计还晚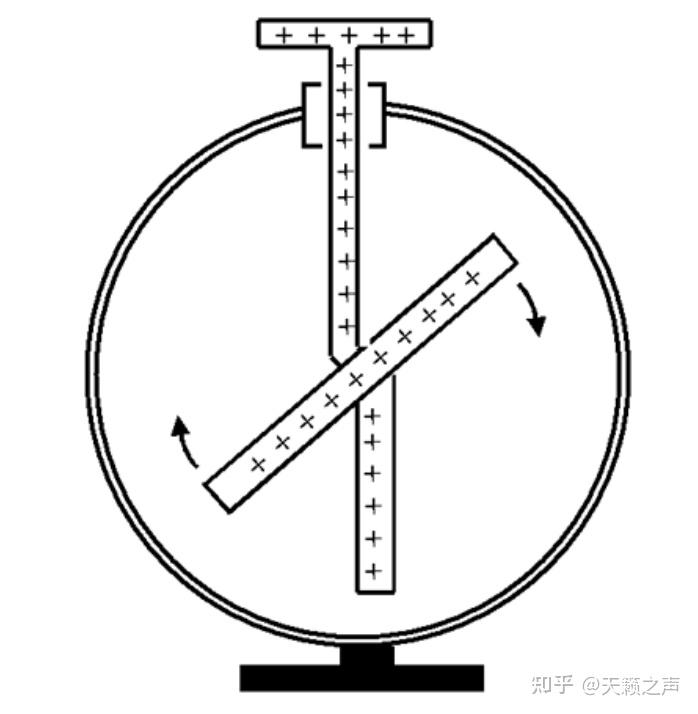，布劳恩静电计不外丈量细小电势差的才能却远远不及汤姆逊象限静电计，它独一的长处就是操做便利，偏转角与电压的二次方成反比[25]

。

Auf diese Weise wird die Ablenkung ansschliesslich von geraden Potenzen der Potentialdifferenz zwischen Gehause und Goldblatt bestimmt, und man ist von der Vertheilung der Potentiale zwischen beiden vollstandig [25]也许是推导太难了，连布莱恩都望洋兴叹，他论文中大篇幅的讨论都没有布劳恩静电计的理论推导，好不容易谈到推导了，推导的都是汤姆逊象限静电计，就是上面我推导的那一串工具。根据布劳恩的那个成果和在金叶验电器阿谁部门的推导，电压是偏转角的1/2次方关系，电容应该随偏转角是一次方的关系，所以电量应该和偏转角是3/2次方的关系----所以在偏转的过程中，电量增长的速度比电容要快。两篇论文除了议论布劳恩静电计外，都花了大篇幅去讨论汤姆逊象限静电计（申明那玩意儿是实好）！固然那个推导挺难的，但还有人知难而上：我举3个推导的例子，固然都不是很尽如人意，

好比周文阳、何海明的”关于静电计三问“那篇文章，里面用到了一个简化，就是”电势差与电场强度成反比“，我评论一下：在电容不发作变革的时候能够那么认为，但是静电计电容的变革现实上是很复杂的，

西南大学从属中学的黄鹏教师在推导静电计电量与偏转角之间关系的时候，接纳量心运动定理，仅仅阐发了量心的受力，但是量心位置有可能变革，但是做者假设其稳定，那个假设也并非很适宜，那种假设其实不合适金箔验电器，倒更合适上面说的通草球静电计和下面的亨雷象限静电计——都在末端有一个带电小球，因为曲径较大，所以电容较大，因而分得了大大都电荷。别的认为金属杆产生的是匀强电场，除非认为金属杆是孤立导体，但现实却会收到指针电量的影响，所以近似其实不尽如人意。

亨雷象限静电计，William Henley 于1770年创造

再好比说陈继桃的”静电计箔叶张角与电势之间的关系“那篇文章，就把指针与金属外壳之间的电场线先近似为圆弧、再近似为曲线，但是如许的近似的合理性值得商榷。也恰是因为他做了那些复杂的近似。因而最末陈继桃利用平行板电容器的电势差公式来对金箔静电计做了尝试定标，得到的关系与布劳恩得到的成果差不多。

Braun在1887年论文里对布劳恩静电计还有进一步的研究：那种静电计在共同目视测微计的情况下，

目视测微计在高达800V时，分辩率能够到达0.1V，若是在4k-6k伏的范畴下分辩率能够到达10V。也就说Braun静电计固然在细小电压的丈量中不如汤姆逊象限静电计，但是在静伏级别（静伏是指静电单元造下的电压单元）的时候也具有比力好的精度，能够在100V-5kV有比力好的丈量特征，也因为它构造上比力简单，所以在丈量大电势差的情况下也会经常利用，也因而遭到了物理教科书的喜爱：因为它能够完成从摩擦起电、静电感应、电介量改动电容以至是欧姆定律的申明。

对了，Braun是谁啊？那小我对阴极射线管做出了很大的奉献，在1897年创造了阴极射线管示波器（不外产生阴极射线的电压需要20000到30000V）。

1909年，因为对无线电报的改良，Braun同创造无线电报的马可尼分享了诺贝尔物理学奖。

那种加拆了显微镜静电计后来也被居里夫人所利用，后来用于研究放射性，是通过静电计的指针归零的时间来度量电离电流。

居里验电器8. 液体静电计 8.1. 毛细管静电计

毛细管静电计自己基于电毛细现象，电毛细现象是由法国物理学家李普曼于1872年所发现，随后李普曼基于电毛细现象创造了李普曼静电计。关于电极系统来说，界面张力不只与界面层的物量构成有关，并且与电极电位有关。那种界面张力随电极电位变革的现象叫做电毛细现象。

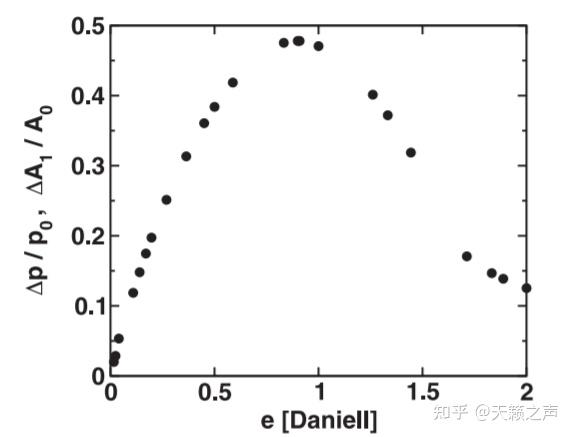电毛细曲线

1872年，李普曼在法国政府的撑持下到海德堡大学进修，在此期间在基尔霍夫的尝试室里工做，李普曼起头专心处置电的研究。其时基尔霍夫的尝试室里有能够检测电荷和电势的汤姆逊象限静电计，李普曼把拆有液态水银电极的毛细管插在硫酸液面上，小心的用象限静电计丈量电荷，尝试安装如下图所示。当他用电池给电极施加电压的时候，水银呈现了上下运动的现象[26]。当增加电池的数量，就能够测定电毛细曲线：外表张力与丹聂耳电池数量的关系[27]。

1873年由李普曼创造的李普曼静电计

毛细管静电计如图所示，与李普曼关于电毛细尝试的办法一致，能够通过显微镜来察看毛细管内水银液面的升高和下降，能够用来丈量电势。那种静电计能够丈量电压仅有丹聂耳单位电动势1/10080的电压，也就是0.1mV的量级。李普曼还创造了一个由水银液面驱动的驱动安装对水银液面的往复运动加以放大。李普曼创造的毛细管静电计还最早应用在了心电图上。后来，德国物理化学家奥斯特瓦尔德改良了那种静电计，用它开展了能斯特的电势理论。1922年，捷克化学家J. 海洛夫斯基（Jaroslav Heyrovský）基于李普曼的毛细研究，创造了测定电解过程物量浓度的极谱法。

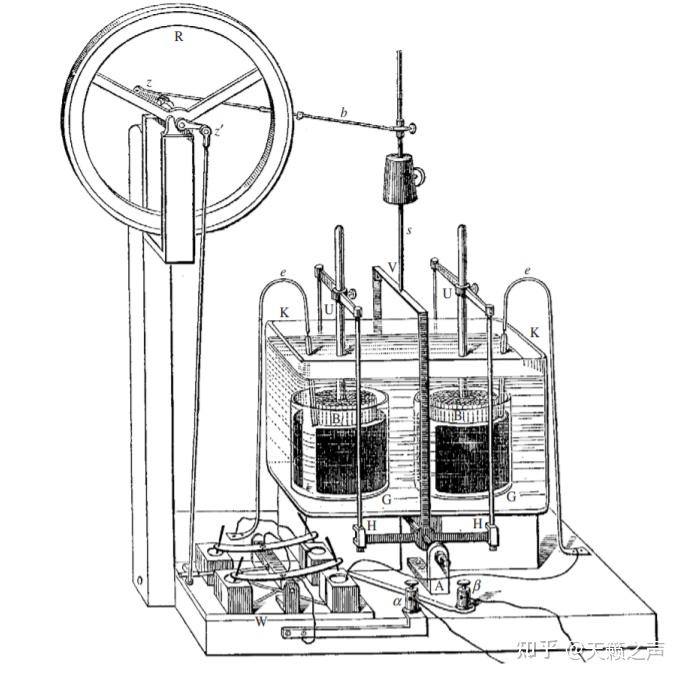察看水银液面运动的驱动安装

1908年，李普曼因为李普曼彩色拍照法，而获得了诺贝尔物理学奖。

8.2. 水银静电计

那种静电计是对上面的汤姆逊绝对静电计的改良，把平行板电容器的下极板和弹簧改成了盛满水银的容器，水银与上极板构成平行板电容器，通过上极板吸引起来的水银重量来平衡静电引力。平衡后，水银液面与上极板的间隔设为d，ρ为水银密度，S为极板面积，h是吸引起来的液面的高度：d和h能够由激光干预仪丈量。

水银静电计的安装

电容器的一个极板的电场强度是： E=\frac{V}{2d} ,

极板与水银的彼此感化力是 F=\frac{VQ}{2d} ，Q=VC

因而 Q=VC=\frac{V\epsilon_{r}S}{4\pi kd} ，静电力就是 F=\frac{V}{2d}·VC=\frac{V^2C}{2d}

所以电势差就是： V =d\sqrt{\frac{8\pi kF}{\epsilon_{r}S }}

按照水银所受电力和重力的二力平衡，因而 F=mg=\rho ghS

所以电势差就是： V =d\sqrt{\frac{8\pi k\rho ghS}{\epsilon_{r}S }} =d\sqrt{\frac{8\pi k\rho gh}{\epsilon_{r} }}

澳大利亚联邦科学与工业研究组织(CSIRO/NML)，1988年用此法绝对丈量电压的不确定度是2.7×10^-7.

参考^ab Volta and the Quantitative Conceptualisation of Electricity: From Electrical Capacity to the Preconception of Ohm’s Law，Jürgen Teichmann^abcA History of Physics from Antiquity to the Enlightenment ,Mario Gliozzi^abcdefg Volta:Science and Culture in the Age of Enlightenment, "Volta’s Science of Electricity CONCEPTION, LABORATORY WORK, AND PUBLIC RECOGNITION"^abBritish Association for the Advancement of Science in 1850 ，“Report on the discussion of Electrical Obervation at Kew”^abcdElectricity in the 17th and 18th Centuries: A Study of Early Modern Physics ，J. L. Heilbron,1857^abcd"Annual Report of the Board of Regents of the Smithsonian Institution",Smithsonian Institution(1857) https://books.google.co.uk/books?id=bc4rAQAAIAAJ&pg=PA378&lpg=PA378&dq=torsion+electrometer+Dellman&source=bl&ots=nKGheKR9At&sig=ACfU3U1H1NwaMwlqLYrwSOrr8lALf7Yllg&hl=zh-TW&sa=X&ved=2ahUKEwjCsrafxKb5AhWgplYBHeCbAG0Q6AF6BAgFEAE#v=onepage&q=torsion%20electrometer%20Dellman&f=false^British Association for the Advancement of Science in 1850 ，“Investigation relating to electricity of atmosphere, made with Peltiers Electrometer”^"Popular Science Monthly",Vol XLI, Edited by William Jay Youmans，1892^"Journal de Physique " , 1801^"电磁学开展史"，宋德生，李国栋，1987^“电磁通论”麦克斯韦，1873^"Reports of the Committee on Electrical Standards(1913)", 220^abcdSitzungsberichte der kaiserlichen Akademie in Wien, April 8, 1886. ON THE GOLD-LEAF ELECTROSCOPE. BY FR. KOLACEK.^Gilb. An.,1806,23^“Ueber die Construction eines Elektrometers,” ibid., (1851)^Pogg.Ann., 1858, 103^"Applications of the Principle of Mechanical Effect to the Measurement of Electro-motive Forces, and of Galvanic Resistances, in Absolute Units", Phil. Mag. Dec. 1851^"Measurement of the Electrostatic Force produced by a Daniells Battery", Professor William Thomson, Jan. 21st, 1860^"Standard Cells: Their Construction, Maintenance and Characteristics",Walter J. Hamer, 1965:pp2^George Green and John T. Lloyd, Kelvin’s Instruments and the Kelvin Museum, Glasgow, 1970, pp. VII and 25-27^"Manual of Electric Instruments", General Electric Corporation, 1949, pages 103-104^Proc. Roy. Soc.,1891, 50, p. 52^电磁学_周毓萃_商务印书馆上海 https://www.doc88.com/p-84659471366633.html^"A Photoelectric Method of Measuring the Light of the Night Sky with studies of the course of Variation through the Night." Lord Rayleigh F. R. S, Received April 3, 1929"^abFerdinand Braun. Ueber das electrische Verhalten des Steinsalzes. Wied. (Drude) Ann. Phys. 31: 856-872; 1887.^G Lippmann, C. R. Séances Acad. Sci., Ser. C, 1873, 1407; Ann Chim Phys, 1875, 494^Electrowetting: from basics to applications, Frieder Mugele and Jean-Christophe Baret，J. Phys.: Condens. Matter 17 (2005) R705–R774