前段时间在chan上看见了两个热门话题:当今世界上有什么样标识符量少少,但很牛逼很典范之做的演算法或工程项目事例?傍边有两个发问是Quake3中的加速逆次方演算法,我本误认为是影片中火神3中再次呈现的标识符,就出格疑惑点进来看了一下,成果实是相联系关系了标识符注解中的一句话“what the *** ?”。
越不会越疑惑,查过之后才晓得那是那款肉搏游戏中的部分标识符,1999年发布,2005年开放源码,距如今已经有20年了,据传那部分标识符再次呈现在公共场所时,几乎惹急了其别人,也是上面那录于标识符:
float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5f; x2 = number * 0.5f; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the *** ? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; }可能将许多开发人员新手都晓得那段牛B的标识符,但关于许多人应该是盲点的。求两个数的次方他们凡是会加进复本的内建体例,也是sqrt,好比说C词汇慧剑两个数的次方依此类推,操纵float(1.0/sqrt(x))方可。
可能将阿谁时候没有sqrt体例,译者被“被逼迫不得已”想到了此种体例,但是最牛逼的是此种体例要比sqrt体例快的多,据传在有的是CPU上能快4倍,也有说快20%的,但我的条记本电脑上校对是要快接近30%,而快的很大原因之一原因在于标识符中的一个个谜样的位数0x5f3759df。上面慎密连系一些相关科学常识和推论来介绍译者几个骚操做,最末的目标都是为了得到那个谜样位数。
起首他们要先明白两个根本科学常识,即浮点数浮点在32位中是若何存储的。32bit能共分为三个部分S、E、M,傍边S只要1位,0则暗示正数、1则暗示正数;E则暗示十进造,共计8位;M则暗示奇数,共计23位,如下表所示图:

以位数4.25为例,有理数5的十进造则暗示为0100;与十进造则暗示有理数反之亦然,十进造也是那般,好比说202^0左侧是2−12^{-1},那么4.25转化成为十进造体例是0100.01。将十进造体例换用科学加减的体例能则暗示为1.0001×22=(1+0.0001)×221.0001\times2^2=(1+0.0001)\times2^2。
那里先用s、e、m则暗示,因为S、E、M另有含义
因为4.25是正数,那么s位就存储为0,然后能将指数处的2+127以十进造体例存储至e中,加上127的理由是将指数的范畴由(-127,128)移码至(0,255),如许就能用指数位置就不消考虑符号问题。最初将十进造点后的0001存储至m中,因为后面的数足以确定十进造点前为1,所以没有需要再存储1,综上是两个浮点数浮点在32位内存中的存储体例,如下表所示图:

所以关于两个要开放的浮点x,有以下则暗示体例,先暂称为存储表达式(那个表达式下文需要加进):
x=(−1)s+(1+m)×2ex = (-1)^s+(1+m)\times 2^e \\
固然e和m则暗示的现实意义是浮点,但是究竟结果十进造是都能转换成十进造的有理数嘛,那么若是从有理数的角度看,有理数E和浮点e、有理数M和浮点m有没有某种关系呢?谜底是必定有的是,但是理由呢我不晓得=.=
E=127+eE = 127+e \\M=1019mM = 10^{19}m \\
加127的原因上文已经介绍了,是为了调整指数的符号范畴;101910^{19}是m中1后所需补零的个数,因为当从浮点角度看时,1右边的0是有起到占位感化的,而若是从有理数角度看时,1右边的0才有现实意义,所以在原根底的m上乘以1后零个数的次幂就能转化成至整M。
他们再回到最后的问题,关于两个浮点x,求它的逆次方:
y=1x=x−12y = \frac{1}{\sqrt{x} \quad} = x^ {- \frac{1}{2}} \\
若是对等式两边同时取对数:
log2y=−12log2xlog_2 y = - \frac{1}{2} log_2x \\
若是慎密连系上面的存储表达式,又能得到两个新的等式:

关于上式中的log2(1+mx)log_2(1+m_x)能绘造出一条光滑的曲线,他们能用曲线y=mxy=m_x比照(如下表所示图),能看见两条线在(0,1)之间十分附近,那么若是再将那条曲线向上平移一点点,能假设那个平移的距为b,那么两条线就有一种近似相等的关系:log2(1+mx)≈mx+blog_2(1+m_x)\approx m_x+b。

需要留意的是此种关系成立的前提是0≤mx≤10\leq m_x\leq 1,经代入得到上面式子:

若是对log2ylog_2 y做不异处置,那么就有上面式子:
my+ey+b≈−12(mx+ex+b)m_y+e_y+b \approx -\frac{1}{2}(m_x+e_x+b) \\
上面他们不是操纵有理数型的M和E别离则暗示m和e嘛,那么天然能用有理数型套用上式中的浮点型,关于差别位数,有理数型和浮点型之间的关系也差别,所以那里同一用常量B和L则暗示,如下表所示:
E=B+eE = B+e \\M=LmM = Lm \\
用有理数型替代浮点型能得到新式子:
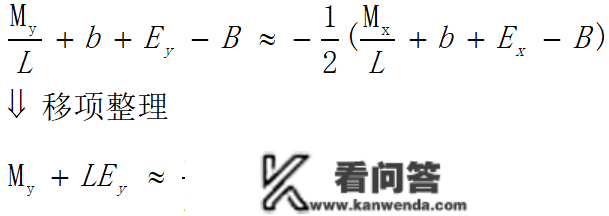
能看见整理后的式子摆布有两个不异的部分M+LEM+LE,他们已经晓得了那三个字母代表的意思,但合在一路表达的又是两个新概念,合并两个有理数是两个很简单的问题,好比说合并33和55,33×100+55=335533\times100+55=3355,那么LE+MLE+M不是那个事理嘛,只不外前者是十进造后者是十进造,所以LE+MLE+M的感化是将M和E存储的位数绑缚在一路,用来则暗示存储的位数,有人想前面不是还有一位S吗?S的感化是则暗示存储位数的正负,根号下的位数必然为正,所以S那位必然为0,没有现实意义。有没有觉得实的秒!
既然那个组合用来则暗示两个位数,那么就能用另两个变量I来则暗示:
Iy≈32L(B−b)−12IxI_y \approx \frac{3}{2}L(B-b) - \frac{1}{2}I_x \\
其实标识符中上面那条语句是套用的那个公式。

标识符中操纵了两个右移运算则暗示公式中的12\frac{1}{2},而32L(B−b)\frac{3}{2}L(B-b)是求出标识符中那串谜样位数的根底,至于怎么求得的,只要译者晓得。后面又有一位大佬对那串位数停止推论,颠末细密的演算求得了一个个新的位数0x5f375a86,它略优于原常数,大佬尽管算,他们跪拜就好。
因为上文中含I的公式是从整型的角度计算的,所以需要强迫类型转换将整形转回浮点型,紧接着最初一行标识符是操纵牛顿迭代法进步成果的切确度,没有什么诧异之处,上面回忆一下上文过程中译者的几个骚操做:
用有理数型则暗示浮点型log2(1+mx)≈mx+blog_2(1+m_x)\approx m_x+b约等关系的替代LE+MLE+M绑缚十进造也许译者操纵的设法是已经存在了很久的理论,但是能把那些理论相组合并灵敏运用缔造出此种新兴高效的演算法,实的不能不感慨一句NiuB,但需要留意的是那个演算法依赖于浮点的存储和字节挨次,所以在Mac上行欠亨。
上面标识符能再精简一些,但是原理一致,只是将一些变量简化:
float InSqrt(float x) { float xhalf = 0.5f * x; int i = *(int*)&x; i = 0x5f3759df - (i>>i); x = *(float*)&i; x = x*(1.5f-xhalf*x*x); return x; }可能将你看见最初仍是那句"what the *** ",究竟结果太多的公式推论都并没有响应的理论根据,只是靠着译者那些脑洞大开的设法,莫非是“我不要你觉得,我只要我觉得?”,关键仍是要领会一 *** 程中几处很牛逼的设法,日常平凡编程中不失为一种法子嘛,也能当成一次科学常识拓展。
