段小宇《讯号与控造系统》和《微分表达式》等专业课程的人常常会被良多难题所疑惑,如:
(1)周期性讯号傅立叶数列中的傅立叶系数力学象征意义是甚么?
(2)频带则暗示甚么?
(3)通过频带他们能晓得甚么?
(4)非周期性性讯号的傅立叶转换到底是甚么意思?傅立叶转换的力学象征意义?
(5)寡数体例的傅立叶转换的力学象征意义?
(6)对讯号用时域阐发有甚么益处?
(7)为甚么周期性讯号的傅立叶转换在响应振幅处呈现冲激表达式?
上述难题虽然看上去有些零星,只不外它们是有联络的,上面,我自始至末把那些难题串起来,文本可能比力多,若是你想晓得成果,则需要你耐心阅读,并希望上面的文本能对你有所帮忙,更详细的文本和应用范畴还请拜见我写的《讯号与建模和应用范畴》一书,本书在人民教育出书社出书。
若是你手里有《讯号与建模和应用范畴》教材,请你存眷“讯号与建模” *** 公家号,那里面列举书中发现的难题。
要晓得傅立叶转换把时域讯号转换为时域表达式(频带),起首需要晓得讯号的频带是甚么。我在教学的时候,规按时域是“讯号”,时域是“表达式”。
出格留意,上面我站在求解“频带”的角度而言难题!
一、周期性讯号或其频带
1、先从周期性讯号说起
周期性讯号的频带则暗示了阿谁周期性讯号所含的大部分不异振幅正弦波讯号的振幅、振幅和初增益那四个“模块”,每个正弦波的那“四个模块”表不雅了阿谁正弦波的全数信息,讯号的频带是用原周期性讯号所含的大部分各振幅正弦波讯号的“三模块”来表不雅原时域讯号的配合构成成份和量纲(傅立叶数列是在时域用正弦波讯号的体例来表不雅周期性讯号的配合构成,出格留意:傅立叶数列是时域的,它的常量是时间t)。
他们不克不及老是意犹未尽地只切磋两个冗杂的时间讯号是由哪些根本讯号合成的,而他们或者说要关心的是阿谁冗杂讯号的“配合构成成份”和那些“成份的量纲”。我十分赞扬网友用的“鸡精”阿谁词,它直抒己见地指出了两个氧化物(相等于时域讯号)和它的配合构成成份或其量纲(频带---讯号鸡精)。能看见,周期性讯号的“鸡精”是配合构成阿谁周期性讯号的各振幅的正弦波的“振幅”、“振幅”和“初增益”那“四个模块”。
如容貌中成药相等于原时域讯号,而它的“药单”相等于其“频带”。
容貌混和好的中成药(相等于两个冗杂讯号),你从上面图中看不出来配合构成它的各成份的量纲。
 容貌混和好的中成药(相等于两个冗杂讯号),你看不出来配合构成它的各成份的量纲
容貌混和好的中成药(相等于两个冗杂讯号),你看不出来配合构成它的各成份的量纲要想晓得它的配合构成成份和量纲,你必然要拿到它的药单。

药单上列举了容貌中成药的配合构成成份和各白附子的“量纲”。对应他们切磋的讯号而言,药草相等于“正弦波讯号的振幅”,总重量相等于“正弦波讯号的振幅”。能看见,阿谁药单图只要“各白附子”和它的总重量,阿谁药单只不外相等于“讯号的振幅谱”。他们也能把各白附子的产地标出(也能理解为正弦波讯号的初增益)。反过来,他们按著“药单”去买药就能构成容貌中成药。
2、傅立叶点数式子(对非周期性性讯号而言是它的傅立叶转换)的了不得之处在哪里?
在那里为甚么我要说“傅立叶点数式子”而不说“傅立叶转换”?因为,求周期性讯号的频带是用傅立叶点数式子,而求非周期性性讯号的频带的式子他们凡是称其为“傅立叶转换”,只不外,傅立叶转换也是傅立叶点数式子。
傅立叶点数式子的了不得之处在于:借助讯号的“共轭性”,通过点数式子能算出原讯号的“鸡精”或者说算出配合构成原讯号大部分不异振幅正弦波(或正弦波)讯号的“三模块”,也是他们在讯号与控造系统专业课程中讲到“频带”。
傅立叶点数式子要完成两个使命:第两个是借助讯号的“共轭性”,从两个“氧化物”(两个冗杂讯号)平分离出此中的两个成份(某一振幅的正弦波),另两个是它像一利为民似的称出被析出的阿谁成份的“量纲”(正弦波的振幅和初增益)。他们不单要晓得两个氧化物的“成份”,还要晓得此中某一成份的“量纲”。所以,傅立叶点数式子兼有“成份热交换器”和“秤”的双重感化。
上面就让他们去看看若何从冗杂讯号平分离出两个正弦波,然后如何算出被析出的阿谁正弦波的振幅和初增益(那是两个或者说了不得的工做)。
3、周期性讯号的则暗示以及它的频带的求解
他们先看看两个周期性讯号的时域则暗示(傅立叶数列),然后就让他们去见证两个了不得的傅立叶点数式子,它是若何算出阿谁周期性讯号的“鸡精”(频带),也是用傅立叶点数式子若何从周期性讯号平分离出两个正弦波以及如何算出阿谁正弦波的振幅和初增益的(那是两个或者说了不得的工做)。
(1)周期性讯号三角表达式体例的傅立叶数列
为了尽快完成上面文本,上面我把我写的《讯号与建模和应用范畴》书上文本间接复造过来,更详细文本还请拜见那本书。
请出格留意:为甚么我把周期性讯号三角表达式体例的傅立叶数列写成上面的体例,而不是式子(4.2-8)的体例?因为只要如许才气充实理解讯号频带以及频带的感化、傅立叶系数、非周期性性确知讯号的傅立叶转换的力学象征意义,才气充实理解我写的上面的文本。

出格要出格留意:所谓的傅立叶数列是在时域则暗示原周期性讯号的配合构成。
由式子(4.2.2)可知:



如许就能计算出两个周期性讯号的频带了(“鸡精”或“药单”)。他们将大部分“三模块”按振幅的位置则暗示出来是原周期性讯号的“频带”了,因而,上面的周期性讯号的傅立叶数列式子才是与“频带”对应的周期性讯号三角表达式体例的傅立叶数列。
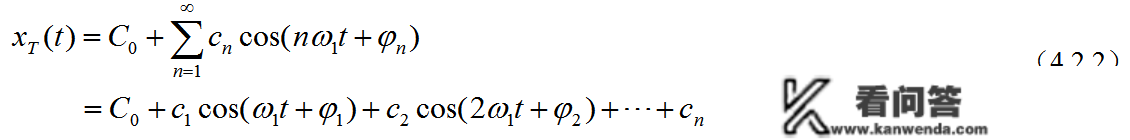
用上面式子则暗示周期性讯号三角表达式体例的傅立叶数列才气更好天文解讯号的“频带”到底则暗示了甚么?以及后面我要说的非周期性性讯号傅立叶转换的“力学象征意义”是甚么,才气更好理解讯号时域阐发的目标。那么,式子(4.2-8)能看做求解讯号频带的中间环节,当然,它也是三角表达式体例的傅立叶数列,只是用它倒霉于理解讯号频带则暗示的文本(也有特殊情况)。
能说,式子(4.2-10)以及(4.2-11)是“最了不得的点数式子”之一。那两个式子为甚么能计算出an和bn?他们需要切磋讯号的共轭性难题。
上面把《讯号与建模和应用范畴》书上文本复造过来。

出格留意:上面点数区间必然在是整倍周期性期间才成立。


如许,上面的点数式子的力学象征意义就很清晰了:




想必各人已经领略到了数学的了不得魔力了吧。
4、周期性讯号配合构成成份的则暗示---讯号频带


能看见,频带图(a)和(b)则暗示了配合构成原周期性讯号的大部分不异振幅正弦波讯号的“振幅”(横坐标)、“振幅”以及“初增益”那四个模块,那与式子(4.2.2)是对应的,那是为甚么我将周期性讯号傅立叶数列写成式子(4.2.2)的底子原因。
讯号频带的感化是用图形(频带图)或式子(向量体例)来则暗示配合构成阿谁周期性讯号的大部分不异振幅的正弦波讯号的“三模块” (振幅、初相和振幅或角振幅),也是说,频带是用“模块”的体例则暗示原讯号的配合构成成份,他们不单要晓得讯号的配合构成成份还要晓得那些成份的份额,那是各人说到的“原讯号的鸡精”。从频带图上,他们就能看见原周期性讯号所含的大部分振幅的正弦波(或正弦波)讯号的振幅和增益的大小,也就晓得了周期性讯号所含的大部分振幅成份以及那些振幅成份对原讯号的奉献大小。上面图(c)是将图(a)和(b)合成两个图(合成的原则请拜见《讯号与建模和应用范畴》书)。
5、周期性讯号复指数体例的傅立叶数列与讯号频带





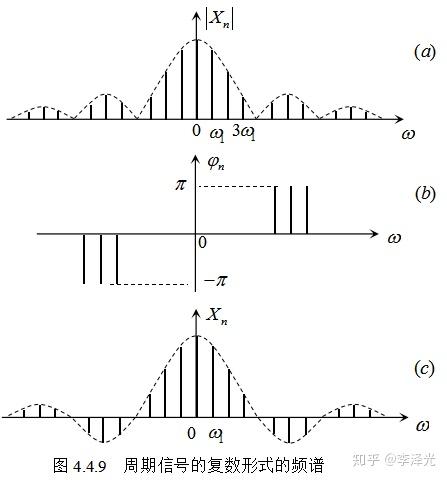
周期性讯号复指数体例傅立叶数列中的傅立叶系数Xn是用寡数的体例则暗示每个正弦波讯号的振幅和初增益信息(包罗正弦波讯号的两个模块)。
必然出格留意:傅立叶系数Xn的点数式子只不外仍是求an和bn(系数为0.5),只是用两个点数式子的实部和虚部一路算出的,它仍是借助“共轭性”,傅立叶系数Xn是寡数体例的原周期性讯号的“频带”(“药单”或“鸡精”)。
出格强调一下:将傅立叶系数Xn的虚部看成是正弦波讯号的初相是不合错误的,它的虚部0.5bn是“正弦波量纲”的振幅信息,不是正弦波讯号的初增益,而正弦波讯号的初相是式子(4.4-17),上面切磋非周期性性讯号傅立叶转换也是阿谁难题,即绝对可积非周期性性讯号的傅立叶转换是两个复表达式,它的虚部也不是肆意角振幅w的正弦波讯号的初增益。
二、非周期性性讯号的傅立叶转换
非周期性性讯号的傅立叶转换是从周期性讯号复指数体例傅立叶数列中的傅立叶系数Xn推导来的(出格留意:不是从傅立叶数列推导来的!),所以,非周期性性讯号的傅立叶转换长短周期性性讯号的“频带”。绝对可积讯号的傅立叶转换是常量为振幅或角振幅的相量表达式,它所含原时域讯号所含的大部分振幅正弦波讯号的“三模块”信息(振幅信息是由傅立叶转换的常量来表不雅的)。但是,绝对可积非周期性性讯号所含的每个正弦波讯号的振幅都趋于无限小,非周期性性讯号的傅立叶转换中的振幅谱是每个正弦波讯号无限小的振幅乘上两个无限大的周期性。若是两个非周期性性讯号是确知讯号,则它的傅立叶转换是两个常量为振幅或角振幅确实知相量表达式(所以,不克不及把它叫做讯号),那申明,阿谁原确知时间讯号所含的大部分振幅正弦波讯号的振幅和初相不是孤立的,他们满足必然关系,阿谁关系是以常量为振幅或角振幅的“时域表达式”。更多文本请参看我写的《讯号与建模和应用范畴》书上第4章和第5章文本。



上面举个讯号的例子:

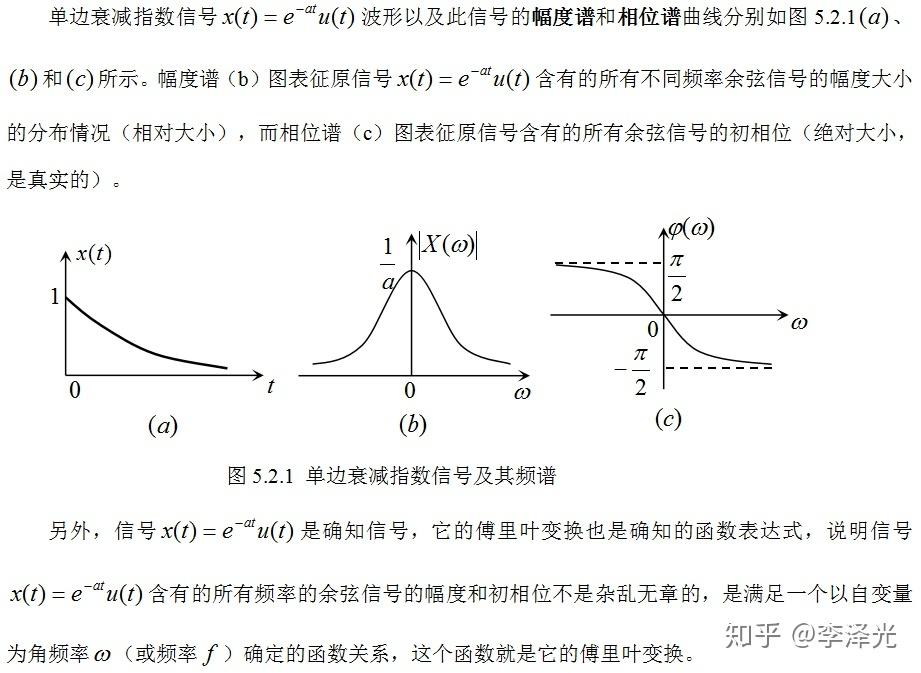
上面是讯号傅立叶转换是复表达式的力学象征意义。上面看看因果不变控造系统的振幅响应的力学象征意义。
因果不变控造系统的振幅响应是此控造系统单元冲激响应的傅立叶转换,因为此控造系统是因果不变控造系统,则其振幅响应也是复表达式。

能看见,讯号的傅立叶转换与控造系统单元冲激响应的傅立叶转换即便都是复表达式,但是,它们的力学象征意义是不异的。
三、周期性讯号的傅立叶转换以及冲激表达式的感化


除了上述对讯号停止傅立叶转换得到讯号的频带以及对控造系统单元冲激响应停止傅立叶转换而得到控造系统振幅响应,那些“傅立叶转换”都有其力学象征意义,人们还发现时域讯号颠末傅立叶转换后在转换域内当时域表达式之间的运算比时域简单,人们借助于时域运算能简化时域里的运算。最初,简单总结一下傅立叶转换:
(1)对讯号停止傅立叶转换得到讯号的频带;
(2)对控造系统单元冲激响应停止傅立叶转换得到控造系统振幅响应;
(3)颠末傅立叶转换后能使运算简单;
若是你手里有《讯号与建模和应用范畴》教材,请你存眷“讯号与建模” *** 公家号,那里面列举书中发现的难题。
目前,已起头逐步把我主讲的“讯号与控造系统”视频课上传到B站上的“李泽光教师”主页上,欢送你存眷并提出定见和建议。
哔哩哔哩 ( ゜- ゜)つロ 乾杯~ Bilibili
