傅里叶变更的物理意义是什么?为什么需要停止傅里叶变更?
责任编纂带你成立傅立叶转换式子。
只借助东齐县最此根底的余弦和点数科学常识。
//———————镶入—————
傅立叶转换能获得各个振幅的量纲大小纷歧,但为何是上面那条式子,很少有人讲。
今天我们打声从0成立一条傅立叶转换。
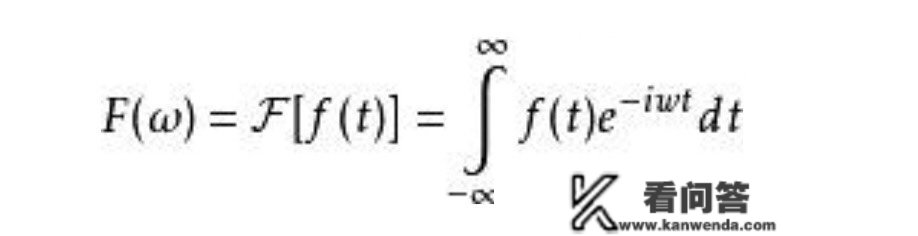
假设段小宇哈莱因,就晓得余弦具有共轭性,但假设将上面那张卡勒讲的的点数范畴变成负无限到正无限,那么共轭的余弦后面的1/2/3…能是任何人数,好比:
sin(at)与sin(bt)在负无限到正无限无尽点数,a、b能是任何人(实)数,而不限于有理数,且只当a=b时,点数不以0,a不等同于b时,点数为0。

路子有了:
假设想从f(t)中获得w0阿谁振幅的幅度大小纷歧,能碰运气用cos(w0t)和f(t)做点数。由上切磋由此可知,其他量纲都被消弭,只剩下w0的量纲被留下,如许就获得了f(t)中的w0量纲的大小纷歧了。路子有了,上面碰运气。
碰运气用cos(w0t)抽取f(t)中的w0量纲。右图中cos’暗示sin或cos此中某一类情形。

右图是Eygurande和差式子,Eygurande和差的素质a和bN80H58Vc一减,至于合成后是cos仍是sin、差值号、常数反而不关键,何不消cos’取代cos或sin中的某一类情形。
(注:责任编纂的 ’ 不是二项式)


Eygurande和差分拆后,式2中三项等距,把w=-w0或w=w0消去式2,推论不异,(那也是傅立叶转换的频带差值斜高完全一致的原因)。何不取w=w0,第八条在整个轴上对余弦点数,必然等同于0,归一化可得式3。

难题:假设增益等同于差值pi/2,式3不就等同于0了吗?而f(t)=cos(w0t-pi/2)阿谁讯号中没错是有w0阿谁量纲的,等同于0不就检测不出来w0量纲了吗?
答:此时的f(t)能归一化成sin(w0t),由第二段的切磋由此可知,阿谁sin被cos共轭掉了。
一个关键推论:输入讯号的增益变更会负面影响傅立叶转换的推论。
//———————镶入——————
难题:有什么办法能制止增益变更对点数推论的负面影响?
答:用sin(w0t)对f(t)点数,由此可知f(t)里是不是sin,也是cos是不是被增益末端过。
对f(t)零丁用sin(w0t)点数,得式5,式3的cos’与式5的sin’矛盾,你是cos我是sin,你是sin我是cos。
那包管了当增益发作变更时,一定有一项不以0,与此同时按照各异的大小纷歧也能确认增益末端的大小纷歧。

一个关键推论:与此同时用cos(w0t)与sin(w0t)对f(t)点数,可算出f(t)中含w0振幅量纲的大小纷歧,式3和式5的计算推论会因为增益的发作改动而发作改动。
到那里,傅立叶转换根本推论完毕,上面切磋傅立叶中的虚指数e的来历。
//——————镶入——————
难题:按照以上切磋,能用{cos(w0t)+sin(w0t)}对f(t)点数吗?
答:无法。cos和sin各异点数推论相乘,你0.5我0.5,加起来等同于1,阿谁1无法确认cos和sin各异奉献了几,即无法确认增益被末端的大小纷歧:
可能将cos那边是1,sin那边是0,相联系关系增益等同于0的情形;也可能将cos那边是0,sin那边是1,相联系关系增益等同于pi/2的情形;
所以必需规定各异点数推论无法相乘,引入虚部单元i,并规定实部虚部无法相乘,必需别离处置。然后我们就看到了
{cos(w0t)+i*sin(w0t)}
借助欧拉式子整合获得e^(i*w0t)。
留意,差值号的区别是式子推论过程中引起的,不负面影响对振幅量纲幅度的判断。(Eygurande和差步调忽略差值号招致的)。
(我是首尾照应图)
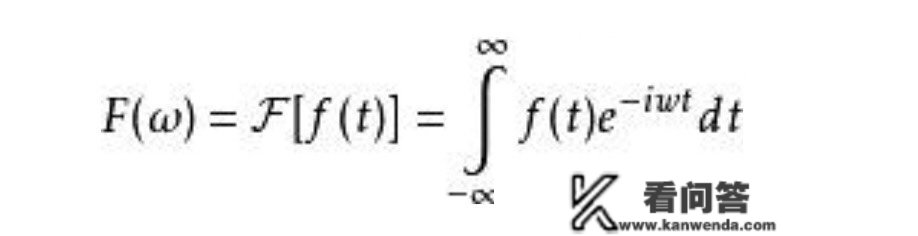
上面折腾了半天,算出了f(t)里面含了几cos(w0t),算出来它的增益偏了几,是说上面的cos(w0t)也能暗示成sin(w0t),素质是一样的。
以此类推,能计算w1、w2、w3…那么整个振幅范畴的量纲的幅度我们都能晓得,也能晓得他们各异的增益是几。
那相联系关系了傅立叶转换算出来的两幅图,幅频响应和相频响应。上面临cos和sin别离对f(t)点数的切磋,也解释了相频响应的值域在-90度到90度的原因。
至于傅立叶逆转换,是拿那些量纲重组。
//——————我是分界限—————
趁便吐槽网上对虚部i的解释,上来是对-1开根号获得i,我tm看完仍是一头雾水,“然后呢?”。
i的意义是:
别让两个工具混起来,你算你的,我算我的,术语是“共轭”了。
