积分电路为什么能够用于电子开关中的延迟？

午睡关键时刻，来发问难题。

========================

他们看右图：

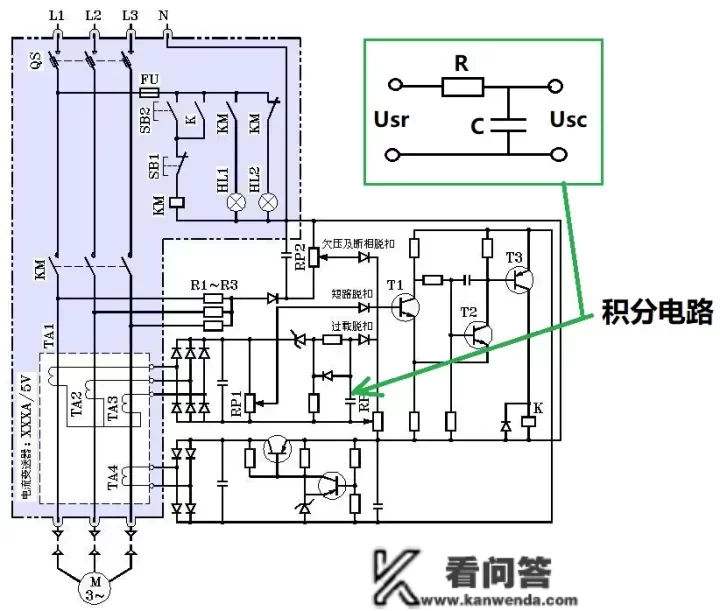图1：点数电路在传动安装Sauxillanges中的应用范畴

图1中他们看见了了点数电路。

他们晓得，电感C等同于用电量Q与电感电阻Uc之比，而用电量Q等同于流往电感的电阻Ic与天数t的平方根，即： C=QUc=IctUcC=\frac{Q}{U_c}=\frac{I_ct}{U_c} 。即便Uc和Ic都是变更的，因而电感的电阻与电阻间有如下表所示关系：

Ic=CdUCdtI_c=C\frac{dU_C}{dt} ，式1

慎密连系图1中左上角的图，他们把电感电阻Uc对天数t点数，然后获得下式：

Usc=Usr(1−e−tRC)U_{sc}=U_{sr}(1-e^{-\frac{t}{RC}}) ，式2

式2是对输入信号Usr点数得来的。

留意到电阻R与电感C的平方根：

RC=UI×QU=UI×ItU=t=TRC=\frac{U}{I}\times\frac{Q}{U}=\frac{U}{I}\times\frac{It}{U}=t=T ，式3

他们把T叫做天数常数，若是电阻的单元是Ω（欧姆），电感的单元是F（法拉），那么T的单元就是秒。则式2酿成：

Usc=Usr(1−e−tT)U_{sc}=U_{sr}(1-e^{-\frac{t}{T}}) ，式4

他们假设在t=0时输入信号Usr由零电平酿成高电平，当t=1RC=1T、2T、3T、4T和5T时，式4输出Ucs会如何变更？

Usc=Usr(1−e−1TT)≈0.6321UsrU_{sc}=U_{sr}(1-e^{-\frac{1T}{T}})\approx 0.6321U_{sr} ,

Usc=Usr(1−e−2TT)≈0.8647UsrU_{sc}=U_{sr}(1-e^{-\frac{2T}{T}})\approx 0.8647U_{sr} ,

Usc=Usr(1−e−3TT)≈0.9502UsrU_{sc}=U_{sr}(1-e^{-\frac{3T}{T}})\approx 0.9502U_{sr} ,

Usc=Usr(1−e−4TT)≈0.9817UsrU_{sc}=U_{sr}(1-e^{-\frac{4T}{T}})\approx 0.9817U_{sr} ,

Usc=Usr(1−e−5TT)≈0.9933UsrU_{sc}=U_{sr}(1-e^{-\frac{5T}{T}})\approx 0.9933U_{sr} ,

右图就是电阻变更的曲线：

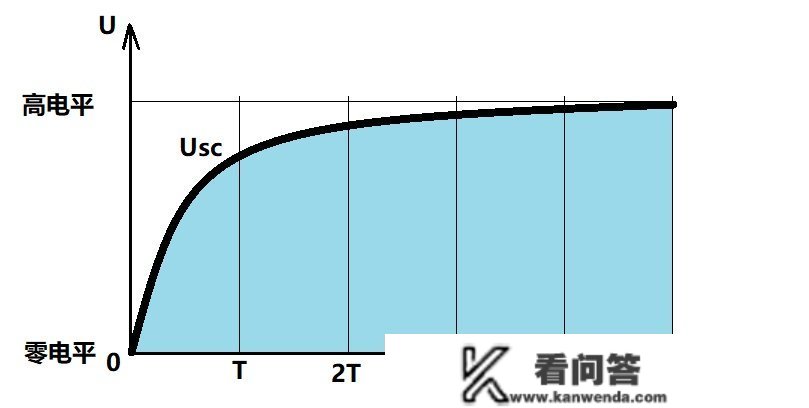图2：电感上电阻上升的情况

由图2可见，电感上的输出电阻抵达高电平需要5T的天数，那就是RC点数电路的延后效应。

关于图1中的点数电路，它的用处就是对外界的过电阻信号产生延后，其实就是线路庇护中的过载长延时L感化。

关于图1，点数电感C对应的天数常数若何计算？他们看见点数电感C的电阻来自于三相电阻互感器的三相电阻，并颠末二极管桥式整流和滤波电感的滤波感化。按电路阐发的原理，规定计算电感天数常数时，把电阻源一律短路电阻源一律开路，因而他们把滤波电感C短路，短路后他们发现，稳压二极管的等效电阻与接零电位的电阻并联，然后再与上端的限流电阻串联，他们设此电阻为R0，则R0C就是电感C所对应的天数常数，点数电路就按此天数常数实现延后。

发问完毕。