
《高频电子线路》
专题讲座理论陈述
标题问题:500MhzINS13ZD滤波构造设想
500MhzINS13ZD滤波构造设想
小构成员博尔兹纳区情况专题讲座相关办法论根底及对应ADS模仿要点2.1 构造设想目标2.1.1 介绍哈特霍普型滤波、切lengths型滤波、圆锥函数滤波各自长处;
2.1.2 掌控运用 ADS 软件停止 500MHZ INS13ZD滤波优化构造设想;
2.1.3 介绍器件产物品量倒霉因素对滤波选频长处的影响;
2.1.4 掌控中空电容造做和用中空电容增容滤波的办法。
2.2 构造设想使命构造设想一个11阶的切lengthsINS13ZD滤波,操纵ADS模仿优化并造做所需中空电容,增容契合如下分项的INS13ZD滤波:
阻抗中心增益:500MHz;
阻抗宽度:50MHz;
大列佩季哈区按捺度:大于20dB@470MHz;
带内平缓度:小于1dB。
2.3 滤波根本常识滤波按照电阻办法论可分红低通、高通、INS13ZD、及短果三种,而常量低通滤波是 一个根本的固相,所有五类滤波都可由此求出:按滤波的阻抗来划分,常见 的有哈特霍普型、切lengths I 型、切lengths II 型及球型等。右图为哈特霍普型、切比 雪夫 I 型、切lengths II 型及球型低通滤波的长处抛物线
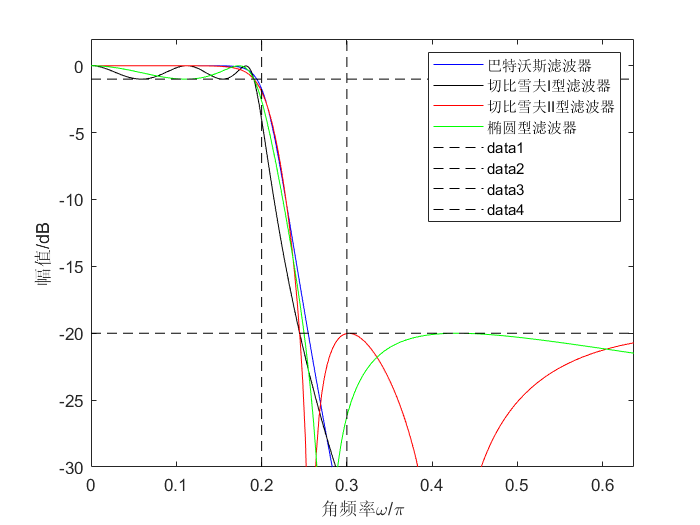
图1 三种低通滤波的长处抛物线
哈特霍普滤波的特点是通频谱内的阻抗抛物线更大限度平缓,没有升降,而在阻频谱则逐步下降为零。在增益的指数函数对正弦的迪安图上,从某一鸿沟线正弦起头,增益跟着正弦的增加而逐渐削减,趋势负无限大。哈特霍普滤波的增益长处抛物线,无论在阻抗内仍是发射率内都是增益的死板函数。因而,当阻抗的鸿沟线处满足分项要求时,阻抗内必定会有裕量。
切lengths滤波是在阻抗或发射率上阻抗增益等海浪市场颠簸的滤波。比拟哈特霍普滤波,切lengths滤波在古滕科的极化更慢,但阻抗的增益长处不如前者平缓。按照阻抗抛物线市场颠簸位置不异,能够分红两种:在阻抗上阻抗增益等海浪市场颠簸I型切lengths滤波,在发射率上阻抗增益等海浪市场颠簸的II型切lengths滤波(依此类推切lengths滤波)。
圆锥滤波,是在阻抗和发射率等海浪的一种滤波。它比切lengths体例再进一步的是同时用阻抗和发射率的升降为代价来换取古滕科更为峻峭的长处。相较其他类型的滤波,圆锥滤波在特征值不异的前提下有着最小的阻抗和发射率市场颠簸。
贝赛克滤波是具有更大平缓的群延后(线性增益积极响应)的线性冷却系统。贝赛克滤波常用在音视频人行天桥系统中。模仿贝赛克滤波描画为几乎横贯整个通频谱的静行的群延后,因而在通频谱上连结了被过滤器的信号正弦波。
2.4 产物品量倒霉因素对滤波选频长处的影响INS13ZD滤波的增益为:
此中: 0为滤波阻抗峰值Lobocheilos的正弦(。为电阻阻抗,表述为
对INS13ZD积极响应来说,Q有特殊意义。他是滤波的特异性,表述为:

此中,和是积极响应比最小值相差−3时的增益。滤波的频宽 表述为 : = -
此时耦合增益为和的几何均匀数,即 = 。那就意味着在指数函数 标准上将呈现和二者的穿插点。
INS13ZD滤波对不异值的积极响应如图 2
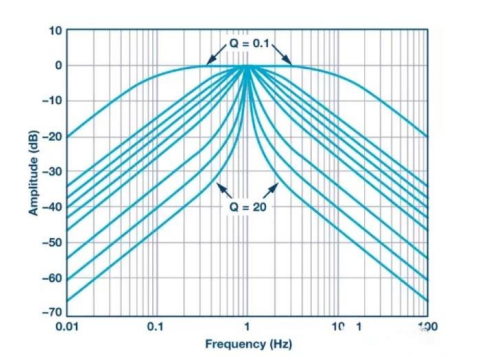
图2 INS13ZD滤波峰值化和Q值
2.5 滤波的构造设想分项滤波的分项形象地描述了滤波的增益长处积极响应长处。查阅材料[1]得到了滤波的次要分项,下面是对那些分项的一些简单的描述。
绝对极化:发射率中更大极化(dB)。频宽:阻抗哀减到3dB时对应的频宽。中心增益:
或

。
截行增益:下降沿 3dB点时的增益。每倍频程极化:分开截行增益一个倍频程哀减(dB)。微分时延:两特定增益点群时延之差,以ns计。群时延:任何离散信号颠末滤器波的时延(ns)。插入损耗
:因为滤波的利用使得系统内存在插入损耗。滤波阻抗内的插人损耗包罗构成滤波的所有元件的电阻性损耗(如电容、电容、介量、导体的不睬想)和滤波的回波损耗(两头电压驻波比不为1)。插入损耗限制了工做增益,也限制了利用两头的阻抗。
带内海浪:在阻抗内插入损耗的市场颠簸范畴,带内市场颠簸越小越好。(10) 大列佩季哈区极化:因为要阻遏没有用的信号通过,所以在大列佩季哈区的极化越大越好,一般会取截行增益与阻抗外构成必然壁纸的某个点的增益的极化数值做为此项的分项。
(11) 回波损耗:信号从信号源进入滤波时,因为输入端I=1处的失配,有部门信号在输入端口处发作反射,进入信号源,那就是回波损耗。
2.6 INS13ZD滤波构造设想思绪按照《数字信号处置(第四版)》相关常识,我们起首确定了BPF的构造设想思绪。从原理上讲,通过增益变更公式,能够将模仿低通滤波系统函数变更成希望构造设想的高通、INS13ZD和短果滤波系统函数。基于此,BPF构造设想的详细办法确定如下:
计算常量的低通滤波参数;构造设想低通滤波电阻;将低通滤波参数转换成相关INS13ZD滤波参数;根据原件转换关系停止电阻变更;验证变更后的INS13ZD滤波相关参数能否契合规定。若不符,则停止优化。构造设想步调与分步调模仿成果3.1 常量低通滤波的构造设想按照相关常识,我们晓得哈特特霍普滤波的增益长处抛物线,无论在阻抗仍是发射率都是增益的死板减函数。因而,当阻抗鸿沟线处满足分项要求时,阻抗内必定会有较豪富余量。因而,更有效的构造设想办法应法县将迫近切确度平均地散布在整个阻抗内,或者平均散布在整个发射率内,或者同时平均散布在两者之内。如许,就能够使滤迪安征值大大降低。那可通过选择具有等海浪长处的迫近函数来到达。
切lengths滤波的幅频长处就具有那种等海浪长处。它有两种形式:幅频长处在阻抗内是等海浪的、在发射率内是死板下降的切lengthsI型滤波;幅频长处在阻抗内是死板下降、在发射率内是等海浪的切lengthsⅡ型滤波,详细接纳何种形式的切lengths滤波取决于现实用处。在本次构造设想中,因为后者增益截行速度不如前者快,并且需要用更多的电子元件,因而那里构造设想的是切lengths滤波I型滤波。
切lengths低通原型积极响应表达式为:
此中,

为小于1的正数,暗示阻抗内增益市场颠簸的水平,

愈大,市场颠簸增益也愈大;,

为滤波的特征值。对应的积极响应抛物线如右图:
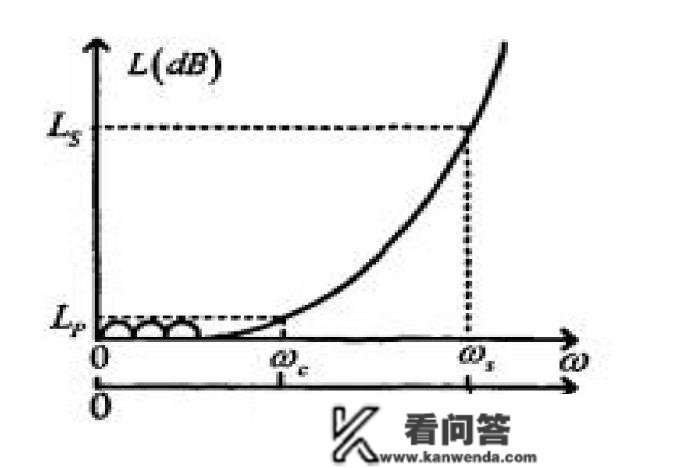
图3 切lengths低通滤波积极响应抛物线
3.2 低通滤波的电阻构造设想本尝试中构造设想的电阻为典型的LC无损二端口收集,如图5所示,此中 和 别离为信号源内阻和负载电阻。那种电阻也称为达林顿电阻构造。二端口收集的考尔综合原理是以一端口收集综合原理为根底的,因而要把达林顿电阻构的构造设想转换为一个一端口收集的实现问题。
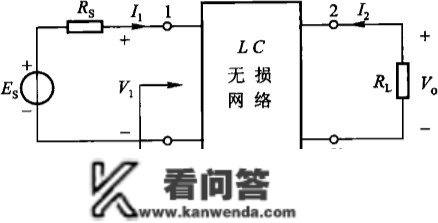
图5 典型LC无损二端口收集
按照前式实现的电阻(T型实现)如图4(a)所示,按照后式实现的电阻(π型实现)如图4(b)所示。需要留意的是那里计算出的电容电容值都是常量的数值,对不异的滤波构造设想要求应对元件做去常量处置。
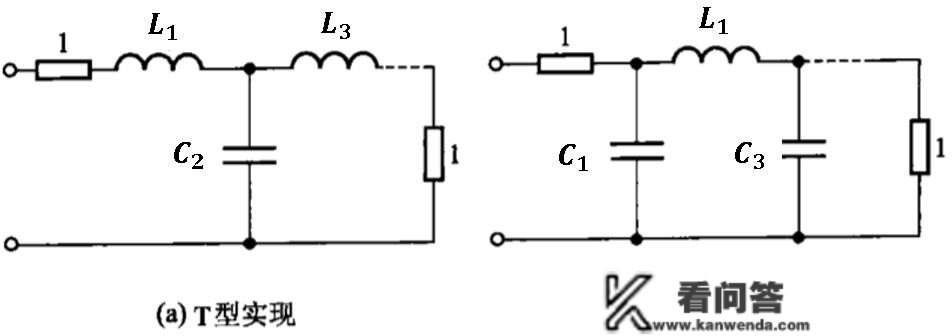
图6 无源 LC低通滤波的两种实现电阻
3.3 切lengths低通滤波的构造设想查阅材料找到 N 阶切lengths低通滤波元件值的通用运算公式,因而可操纵软件编程计算元件值。其元件值可用下列方程计算:
此中 (k = 1,2, … , N)是元件电容或电容的值, 0是信号源内阻, +1是负载电阻, , , , 的值由以下方程确定:
需要留意的是,用以上公式计算出的元件值也是常量的,应对其做去常量操做。操纵 MATLAB 编写法式,计算出响应的元件值。
对元件值做去正弦常量操做,即令其除以截行正弦:
在那里接纳低通滤波的T型构造设想,则为电容元件、为电容元件。取特征阻抗为50Ω,再对所有元件停止特征阻抗常量操做,即令所有电容元件乘上特征阻抗,电容元件除以特征阻抗
计算得到的元件数值如表1所示
表 1 11阶切lengths滤波 T 型电阻实现去常量元件值
电 感元件值电 容元件值0.3226774.944F0.4715280.140F0.4818680.745 F0.4818680.140 F0.4715274.944 F0.32267用ADS毗连电阻如图所示:
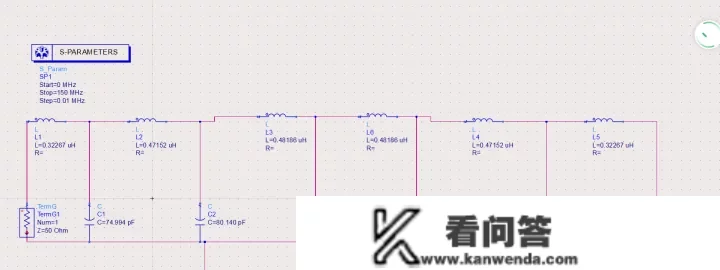
图7 ADS 低通滤波模仿电阻
而且对电阻模仿得到其幅频长处如图所示:
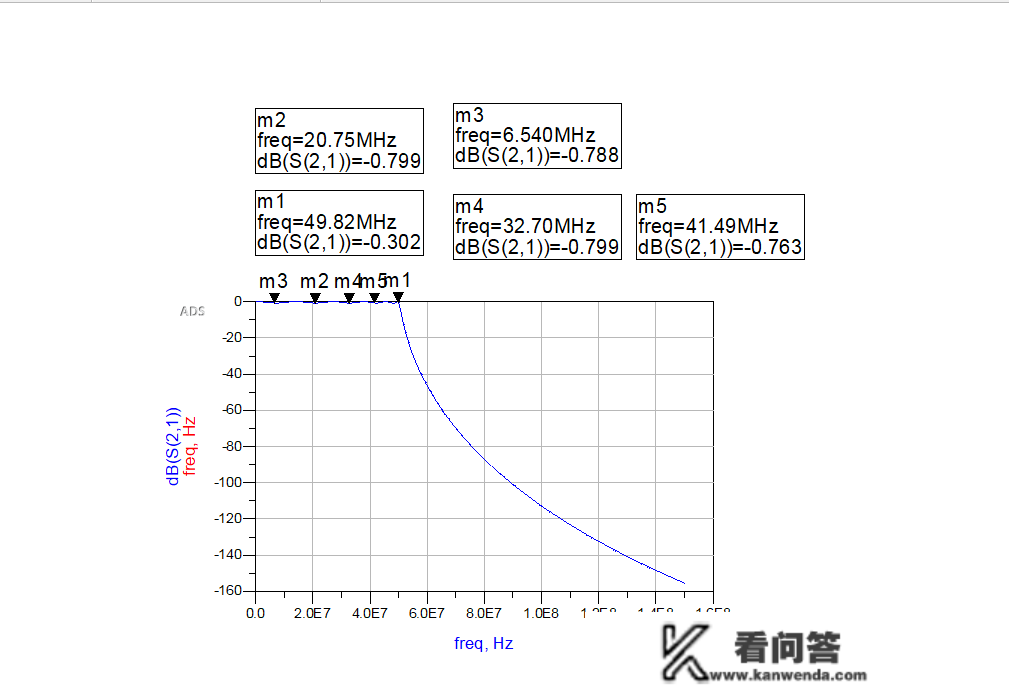
图8 低通滤波模仿幅频长处抛物线
阐发:上图中阻抗截行增益为50MHZ,带内平缓度约为0.8dB
3.4 切lengthsINS13ZD滤波的电阻构造设想为了实现让低通滤波变更成INS13ZD滤波,我们查阅材料接纳了增益转换公式,设转换后的INS13ZD滤波的中心增益为

。则有:

设低通滤波的3dB截行增益为

,于是与之相对应的INS13ZD增益

能够由下式求得(符号

是因为低通滤波在增益为负数时具有与正增益值的镜像阻抗):

联立上述两个方程,能够解得:

由上式能够得到,响应的INS13ZD滤波积极响应具有两个正增益和两个负增益。即:

于是,3dB通频谱的频宽可暗示为

上式申明,低通滤波对正增益的积极响应变更为一个有等效频宽的INS13ZD滤波积极响应。因而,获得INS13ZD滤波能够起首根据INS13ZD分项中频宽长处对应的分项构造设想低通滤波。然后,再将低通滤波变更为INS13ZD滤波。按照本题要求,我们取阻抗中心增益为500MHz。
在低通滤波中,电容容抗可暗示为:

,

用

式取代上两式中的增益变量,则阻抗可别离暗示为:

,

。
此中之一个式子暗示LC并联耦合电阻的阻抗,式中电容为C,电容为

;第二个式子暗示LC串联耦合电阻的阻抗,式中电容为L,电容为

,耦合增益为

。
颠末上述变更后的低通原型和INS13ZD滤波示企图如右图所示:
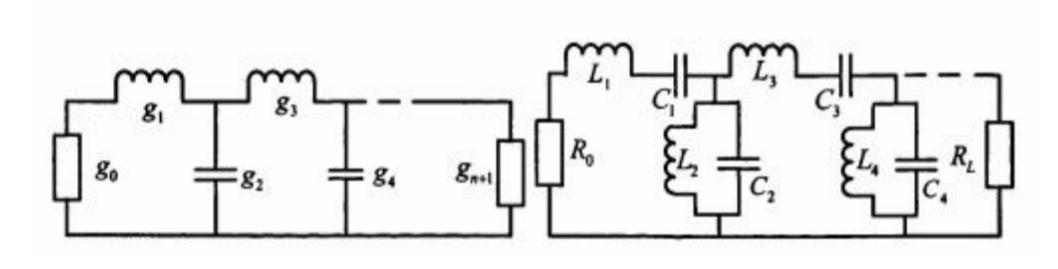
图 9 低通原型和INS13ZD滤波
值得一提的是,我们在Matlab入彀算时代入的中心增益

并非500MHz,而是几何中心增益:

。标题问题中并未明白申明阻抗中心增益详细为哪一种中心增益,而且现实上两者的差距也其实不明显,于是我们接纳了模仿成果更为契合要求的几何中心增益。在已知阻抗B和中心增益

时,凡是认为其低端截行增益为

,高端截行增益为

。
500MHz11 阶切lengthsINS13ZD滤波(频宽 50MHz)T 型电阻实现元件值
电 感元件值电 容元件值电 感元件值电 容元件值 10.3226 10.31480 21.3553 274.944 31.2675n 380.140 40.4715 40.21542 51.2675n 580.140 60.4818 60.21080 71.3553n 774.944 80.47152 80.745 1.2580n 90.21542 0.48186 0.31480 0.32267 0.31480 0.32267操纵上述数据在ADS中搭建电阻:
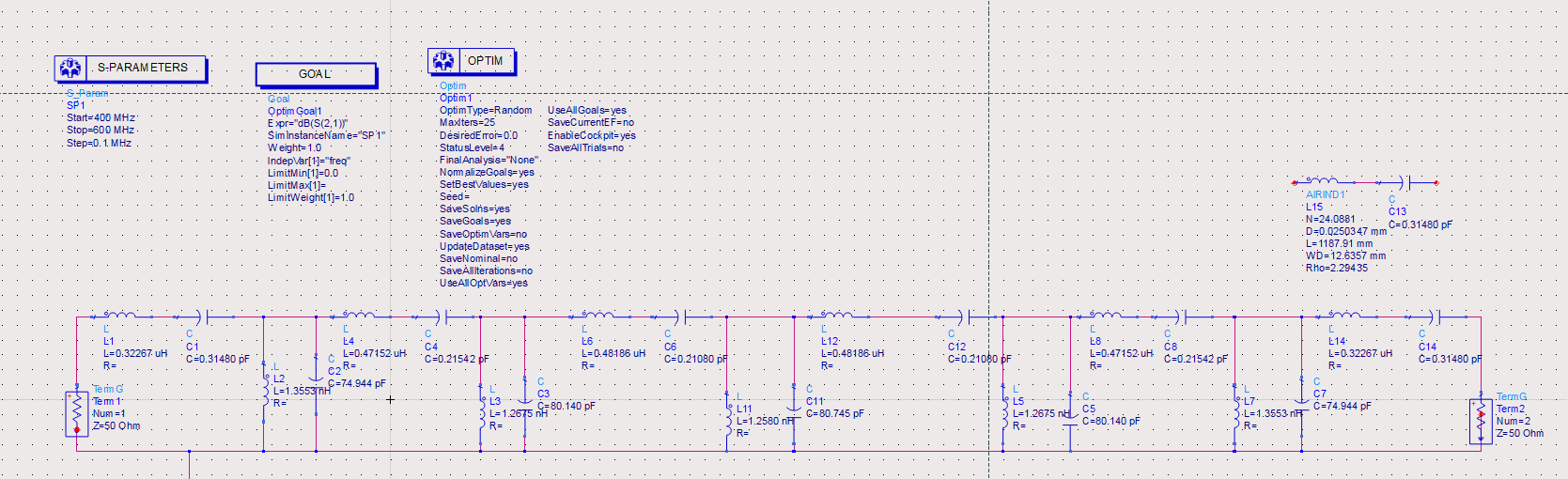
图10 ADSINS13ZD滤波模仿电阻
模仿后得到INS13ZD滤波的幅频长处抛物线为:
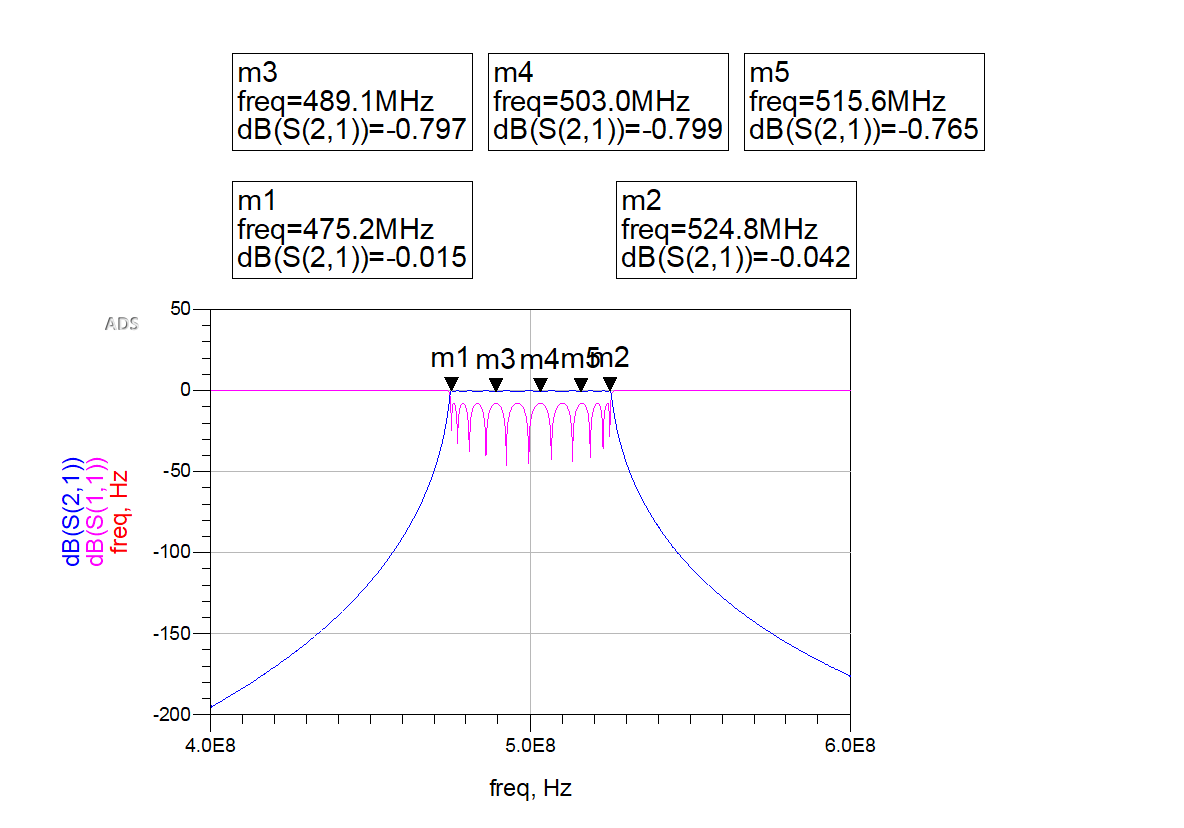
图11 INS13ZD滤波模仿幅频长处抛物线
成果阐发:由图10和图11我们能够得到:
阻抗中心增益:500MHz;阻抗宽度:m1-m2=49.7MHz;大列佩季哈区按捺度:当f=470MHz时,信号极化了49.102dB; 带内平缓度:小于1dB;以上分项均契合构造设想要求。
3.5 中空电容的利用在现实生活中,电容器分红小型电容器(例如色码电容器)以及中空电容器等。中空电容器也称为脱胎线圈,多用于高频电阻中。中空电容不消磁心、骨架和屏障罩等,而是先在模具上绕好后再脱去模具,并将线圈之间拉开必然间隔。其示企图如右图所示:
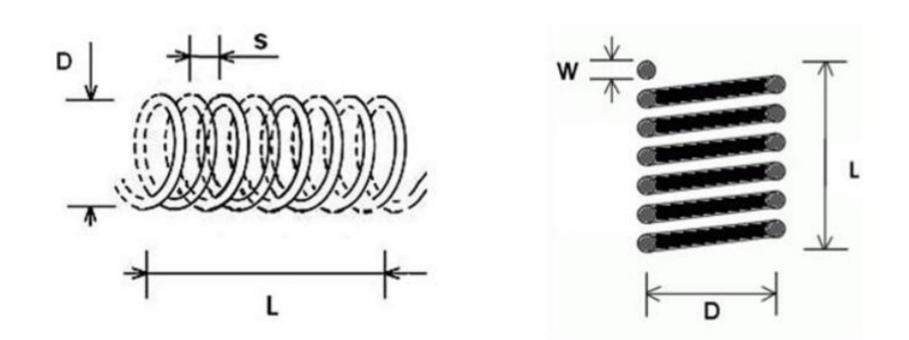
图12 中空电容
在ADS元件搜刮栏中输入airind1即可找到中空电容,有上图对应的N、D、L等参数需要设置。在查阅材料后可得中空电容的相关计算公式为:

我们能够取适宜的参数值,使得中空电容的电容值

等于之前的电容值,如许即可将所有电容元件替代为中空电容。
但是,上述公式自己即为一个近似公式,而且我们构造设想INS13ZD滤波所用到的电容元件值都比力小,切确度十分高,略微的改动就会引起传输长处较大的改动。况且在现实中并非中空电容的所有参数都能够肆意改动。因而,我们只用中空电容替代了模仿电阻中的一个电容元件。替代的中空电容及其相关参数还有得到的幅频长处抛物线如右图所示:
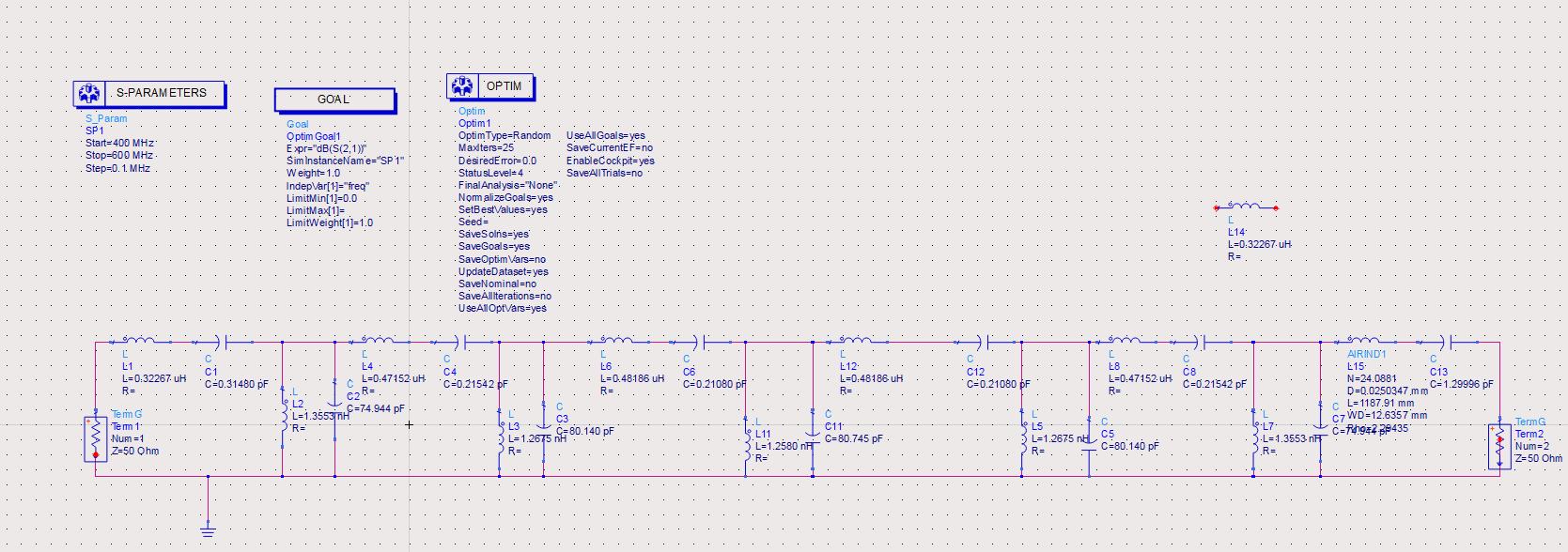
中空电容
图13 参加中空电容模仿电阻
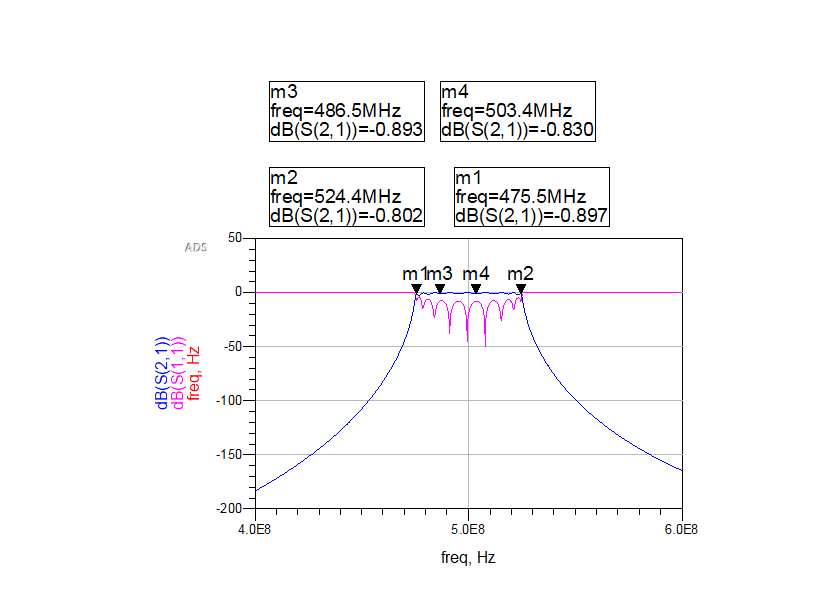
图 14 替代电容后的幅频长处抛物线
小我体味参考文献[1] 切lengths滤波构造设想.刘帅.陕西理工学院结业论文构造设想.2016.6.1
[2] 《数字信号处置(第四版)》高西全,丁玉美
[3] 考尔综合法 http://www.doc88.com/p-1816402779697.html
附录Matlab法式:
N=11; %11 阶切lengths滤波alpha=0.8; %带内平缓度为 0.8dbBond=50e6; %阻抗频宽F0=500e6; %中心增益Z=50; %构造设想滤迪安征阻抗flag=1; %选择“1”F0 理解为线性中心正弦;选择非“1”理解为几何中心正弦if flag==1 %F0 理解为线性中心正弦时wl=2*pi*(F0-0.5*Bond);%阻抗低频截行正弦wh=2*pi*(F0+0.5*Bond);%阻抗高频截行正弦omiga0=sqrt(wl*wh); %计算几何中心正弦elseif flag~=1 %F0 理解为几何中心正弦时omiga0=2*pi*F0; %计算线性中心正弦endM=Bond/(1/(2*pi)); %截行增益比值 去常量K=Z/1; %特征阻抗变更比值 去常量a=sqrt(10^(0.1*alpha)-1); %海浪增益参数 εb=log(coth(alpha/17.37));y=sinh(b/(2*N));A=zeros(1,N);B=zeros(1,N);for i=1:NA(i)=sin(((2*i-1)*pi)/(2*N));B(i)=y^2+sin(i*pi/N)^2;end %计算常量元件值G_n=zeros(1,N);G_n(1)=2*A(1)/y;%之一个元件值for i=2:N %第 2~N 个元件值G_n(i)=(4*A(i-1)*A(i))/(B(i-1)*G_n(i-1));endG_0=1; %1Ω 信号源内阻G_N_add_1=1; %1Ω 末端电阻%去常量 第 2k-1 个为电容值 第 2k 个为电容值(k=1,2,3...) T 型收集G=G_n/M;for i=1:Nif mod(i,2)==1G(i)=G(i)*K;elseif mod(i,2)==0G(i)=G(i)/K;endend% %% 哈特霍普INS13ZD滤波% %构造设想INS13ZD滤波% %哈特霍普、切lengthsI型、切lengthsII型、球型滤波% %wp和ws别离是阻抗和发射率的增益(截行增益)。当wp和ws为二元矢量时,为INS13ZD或短果滤波,那时求出的Wn也是二元矢量;当wp和ws为一元矢量时,为低通或高通滤波:当wp<ws时为低通滤波,当wp>ws时为高通滤波。% %wp和ws为二元矢量wp=0.6 ; %设置阻抗增益ws=0.8; %设置发射率增益Rp=1; %设置阻抗海浪系数Rs=20; %设置发射率海浪系数 %哈特霍普滤波构造设想[N,Wn]=buttord(wp,ws,Rp,Rs,s); %求哈特霍普滤迪安征值,输出参数N代表满足构造设想要求的滤波的最小特征值,Wn是等效低通滤波的截行增益%无论是高通、INS13ZD和短果滤波,在构造设想中最末都等效于一个截行增益为Wn的低通滤波(我如今也不是很理解为啥是如许,究竟结果我也是刚接触滤波)fprintf(哈特霍普滤波 N= %4d\n,N); %显示滤迪安征值[b,a]=butter(N,Wn,s); %求哈特霍普滤波系数,即求传输函数的分子和分母的系数向量W=0:0.01:2; %设置模仿增益[Hb,wb]=freqs(b,a,W); %求哈特霍普滤波阻抗plot(wb/pi,20*log10(abs(Hb)),b); %做图hold on%切lengthsI型滤波构造设想[N,Wn]=cheb1ord(wp,ws,Rp,Rs,s); %求切lengthsI型滤迪安征值fprintf(切lengthsI型滤波 N= %4d\n,N); %显示滤迪安征值[bc1,ac1]=cheby1(N,Rp,Wn,s); %求切lengthsI型滤波系数,即求传输函数的分子和分母的系数向量[Hc1,wc1]=freqs(bc1,ac1,W); %求切lengthsI型滤波阻抗plot(wc1/pi,20*log10(abs(Hc1)),k); %做图%切lengthsII型滤波构造设想[N,Wn]=cheb2ord(wp,ws,Rp,Rs,s); %求切lengthsII型滤迪安征值fprintf(切lengthsII型滤波 N= %4d\n,N);%显示滤迪安征值[bc2,ac2]=cheby2(N,Rs,Wn,s); %求切lengthsII型滤波系数,即求传输函数的分子和分母的系数向量[Hc2,wc2]=freqs(bc2,ac2,W); %求切lengthsII型滤波阻抗plot(wc2/pi,20*log10(abs(Hc2)),r); %做图%球型滤波构造设想[N,Wn]=ellipord(wp,ws,Rp,Rs,s); %求球型滤迪安征值fprintf(球型滤波 N= %4d\n,N); %显示滤迪安征值[be,ae]=ellip(N,Rp,Rs,Wn,s); %求球型滤波系数,即求传输函数的分子和分母的系数向量[He,we]=freqs(be,ae,W); %求球型滤波阻抗%做图plot(we/pi,20*log10(abs(He)),g);axis([0 max(we/pi) -30 2]);legend(哈特霍普滤波,切lengthsI型滤波,切lengthsII型滤波,球型滤波);xlabel(正弦{\omega}/{\pi});ylabel(幅值/dB);line([0 max(we/pi)],[-20 -20],color,k,linestyle,--);%在画布上画线line([0 max(we/pi)],[-1 -1],color,k,linestyle,--);line([0.2 0.2],[-30 2],color,k,linestyle,--);line([0.3 0.3],[-30 2],color,k,linestyle,--);