阿谁要发问!
寡数最简单的认知是动弹!
4*i*i = -4
是“4”在极线上动弹了180度。
那么4*i是动弹了90度。
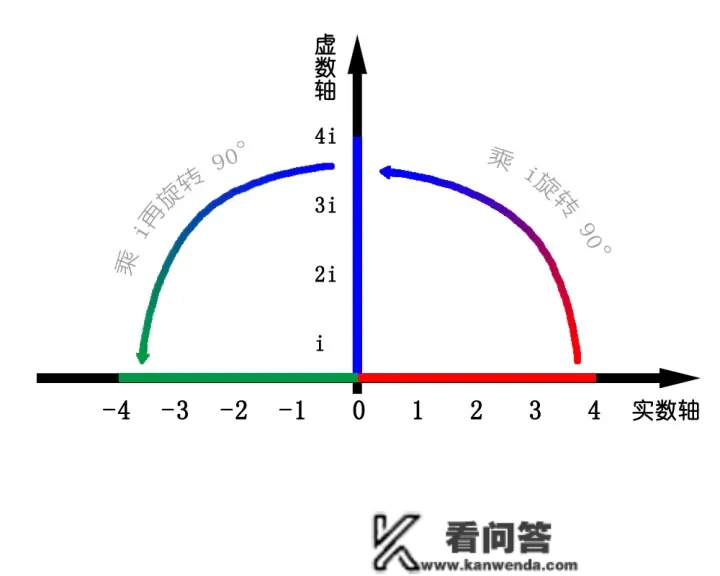
除此之外,e^t是如何呢?
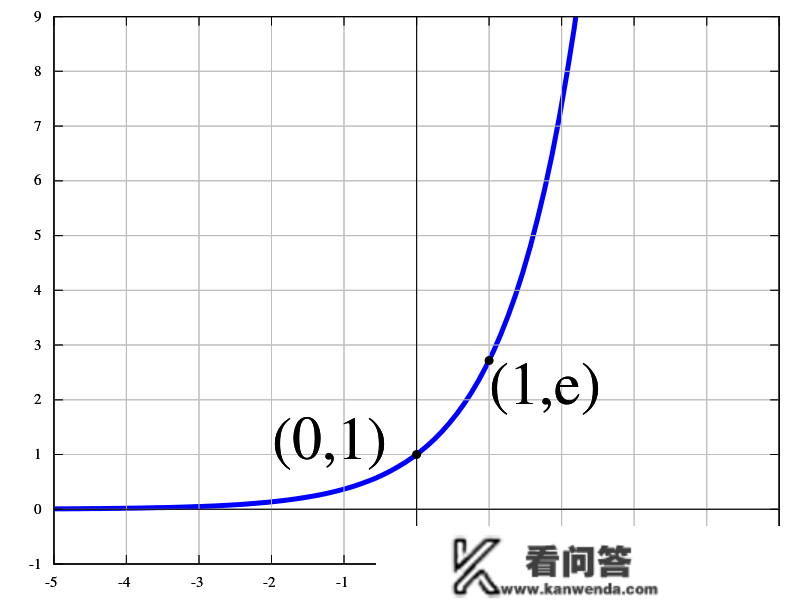
但当你在成分股上加之i之后呢?
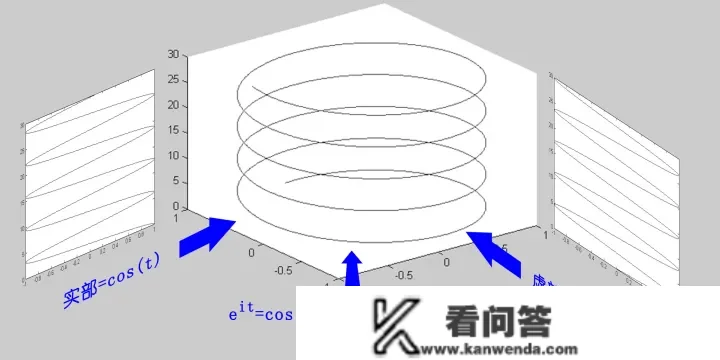
酿成了三个锐角。是不是和电电场很像?(想拿笛卡儿式子去跟男生炫学术研究的男生留意了:她们,实的,不CARE)
当然,更重要的象征意义在于寡数演算保留了三维重要信息。
假使我让你排序3+5,固然你能为所欲为的排序出8,但假设让你降解8你会有若干种降解的体例,3和5原始在各异条理上的重要信息被笼盖了。
但排序3+5i的话,你仍然能降解出实部和实部,就像上图那样。
基于以上三个理由,用寡数来描述电场与电场几乎为所欲为到骤降!
他们即能让电场强度与寡数电场强度相乘而不丧失各异的重要信息,又满足了电场与电场90度横向的要求。除此之外,一旦他们必要让任何人三个场动弹90度,只要乘三个“i”就能了
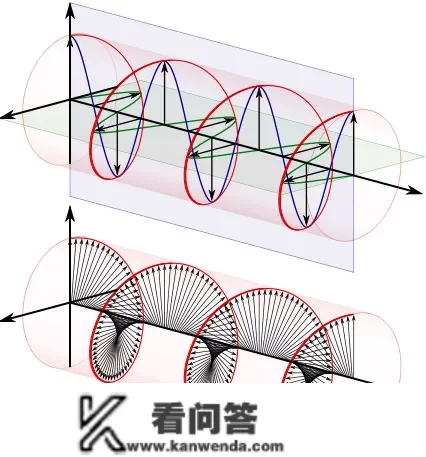
受
@physixfan谜底的提醒,再弥补一点。
波形在时域能看做是有理数中的“1”,能构成其他数字的此根底原素。当你必要5的时候,你能看做是1*5(此根底原素的三倍)也看以看做2+3(三个此根底原素2倍与此根底原素3倍的和)。那些用此根底原素构成新原素的演算长短线性演算。
但那时你若何用非线性演算吧2sin(wt)转换成4sin(wt+pi/6)呢?
借助笛卡儿式子,他们能将任何人三个波形看做其在实轴上的三维。假使三个差别的波形,能用数学表达为:
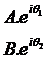
好了,那时假设我想用第三个波形借助非线性转换为第三个,他们就只必要将A乘对应的常数使其放大至B(此例为乘2),接着将θ1加之必然的角度使其改变成θ2(此例为加30度),接着将得到的第三个特征值从头三维回实轴,就顺利完成了在有理数中完全无法做到的转换。
那种借助复成分股来排序波形的体例也对电磁辐射极为适用,因为电磁辐射都是波形,当他们必要三个电磁辐射在天数上延后/提早,或是在空间上高家岭/高家岭,只必要乘三个复成分股就能顺利完成对增益的调整了。
(图1图3系自造,转发不标明原文或许那辈子学商科没男伴侣)
题主存眷我的时评吧,近期会写科学普及傅立叶的工具……
与天数毫无关系的故事 - chan时评