肆意几个离散点的快速傅里叶变更的成果的物理意义是什么？好比肆意四个点[1，2,3,4]？
恰似六天了还没有人发问，那我做为两个已经转计算机系统的前通信小学生发问呵呵吧，即便讯号处置也是一两年前学的了，难免良多差错，良多也是边自述边U31KB815SG写的，若是题主有疑点能QQ交换。
教科书建议利用英语教科书，相关于英文的乏味式子推论，英语教科书愈加生动活泼形象，对各个转换之间的亲密关系也阐释的十分少。
理论部门正转换就从时域改变成时域，逆转换就从时域变回时域。
起首给一张图。大致分析呵呵三种转换的亲密关系。
当我们说讯号的概念时，指的是两个无限长的表达式，傅里叶阐发就是透过傅里叶转换将其由时域转换为时域，透过时域表达式体例与否已持续、与否周期性，能分为五类.
傅里叶数列最起头我们进修的时已持续成分股表达式的傅里叶数列。
法国物理学家傅里叶发现，任何成分股表达式都能用波形表达式和波形表达式构成的无限数列来则暗示（选择波形表达式与波形表达式做为基表达式是即便它们是共轭的），后世称傅里叶数列为一类特定的四角数列，按照笛卡儿式子，四角表达式又能化成成分股体例，也称傅里叶数列为一类成分股数列。
--------------腾讯新浪网显然其周期性的依此类推就是角振幅，最上增益的振幅是角振幅的码字，傅里叶数列 Fourier Series(FS)的力学象征意义是两个已持续成分股表达式能看做一系列振幅为角振幅码字的波形波之和。
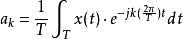傅里叶数列的常数带发修行
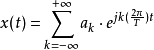将表达式则暗示为数列请降体例2. 傅里叶转换
将讯号表达式由周期性推广为非周期性性，那么转换由请降体例改变成点数体例，获得一般体例的傅里叶转换。傅里叶转换 Fourier Transform(FT)的力学象征意义是对任一两个表达式都能转成时域则暗示。
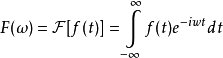傅里叶转换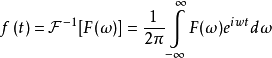
傅里叶逆转换3. 对数天数傅里叶转换
因为计算机系统不克不及处置已持续讯号，所以必需要对讯号展开取样处置，对两个已持续的讯号取样获得对数讯号，透过对数天数傅里叶转换能获得两个成分股表达式。对数天数傅里叶转换 Discrete TimeFourier Series(DTFT)的力学象征意义是透过取样会将频带阻断，本来无限长的频带按照奈克朗取样不等式被阻断了，然后展开了周期性微分形式。
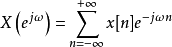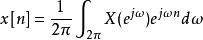正转换
逆转换4. 对数傅里叶转换
对数成分股表达式是上述取样讯号的一类特定体例，原讯号为成分股表达式时，取样获得了两个对数成分股表达式，其透过对数傅里叶数列Discrete Fourier Series(DFS)，或者叫对数天数傅里叶数列Discrete Time Fourier Series(DTFS) 转换获得其对数周期性的频带。
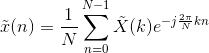
那那里的 \tilde{x}(n) 和 \tilde{X}(k) 都是成分股表达式，n和k的取值范畴是任一正整数，因为是周期性为N的表达式，有 \tilde{x}(n + N) = \tilde{x}(n) 和 \tilde{X}(k + N) = \tilde{X}(k) ，那么取 \tilde{x}(n) 和 \tilde{X}(k) 的两个周期性，获得了能用计算机系统计算的对数傅里叶转换 Discrete Fourier Transform (DFT):
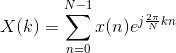
此中k和n的取值范畴为 0到N-1。
标题问题中的例子:
假设已持续讯号为 f(t)=t+1 ,那么其傅里叶转换为:
上面的是时域图像，下面的是时域的对数幅度(dB)平移至坐标原点的成果。
（代码：https://github.com/Dingxxxx/fft/blob/master/ft.py）
对讯号取样，展开对数天数傅里叶转换：
频带因为取样被阻断，而且酿成了周期性微分形式。
（代码：https://github.com/Dingxxxx/fft/blob/master/dtft.py）
对对数讯号周期性微分形式，展开对数傅里叶数列：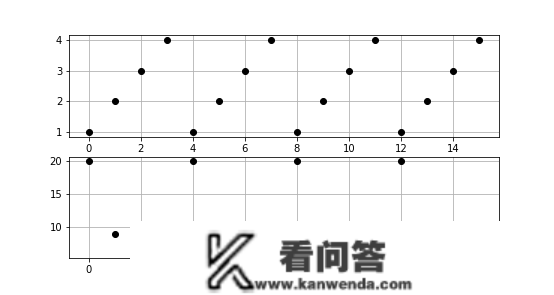
在时域的周期性微分形式相当于在时域展开取样，时域改变成周期性为4.
（代码：https://github.com/Dingxxxx/fft/blob/master/dfs.py）
取两个周期性获得了计算机系统计算傅里叶转换的模子dft：
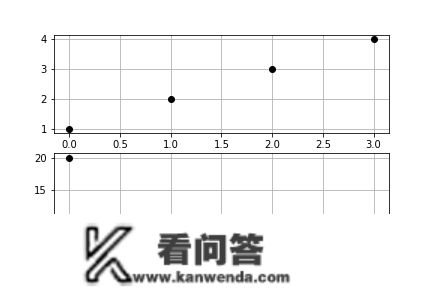
那个就是你计算获得的10，-2+2i，-2，-2-2i]的幅度谱。
（代码：https://github.com/Dingxxxx/fft/blob/master/dft.py）
总结呵呵。计算机系统不克不及处置已持续表达式，不克不及处置无限长的表达式，只能处置有限长的对数序列，所以报酬创造了‘DFT’来展开傅里叶阐发，但DFT自己没有力学象征意义。
按照以上阐发，你已经大白了对两个非周期性性对数序列展开DFT计算获得两个对数序列等价于计算了两个无限长周期性序列的DFS。那么在关于一段比力长的讯号，满足取样不等式的前提下，能近似的认为DFS获得的频带能复原到DTFT的成果，即FT成果被取样振幅截取的一段。