【视频】随机颠簸率SV模子原理和Python对标普SP500股票指数揣测|附代码数据
全文链接:
比来我们被客户要求撰写关于随机颠簸率SV模子的研究陈述,包罗一些图形和统计输出。
什么是随机颠簸率?随机颠簸率 (SV) 是指资产价格的颠簸率是改变的而不是恒定的
“随机”一词意味着某些变量是随机确定的,无法切确揣测。

在金融建模的布景下,随机建模迭代随机变量的持续值,那些值相互不独立。非独立的意思是固然变量的值会随机改变,但其起点将取决于其先前的值,因而取决于其先前的值,依此类推;那描述了所谓的随机游走。
点击题目查阅往期内容

展开全文
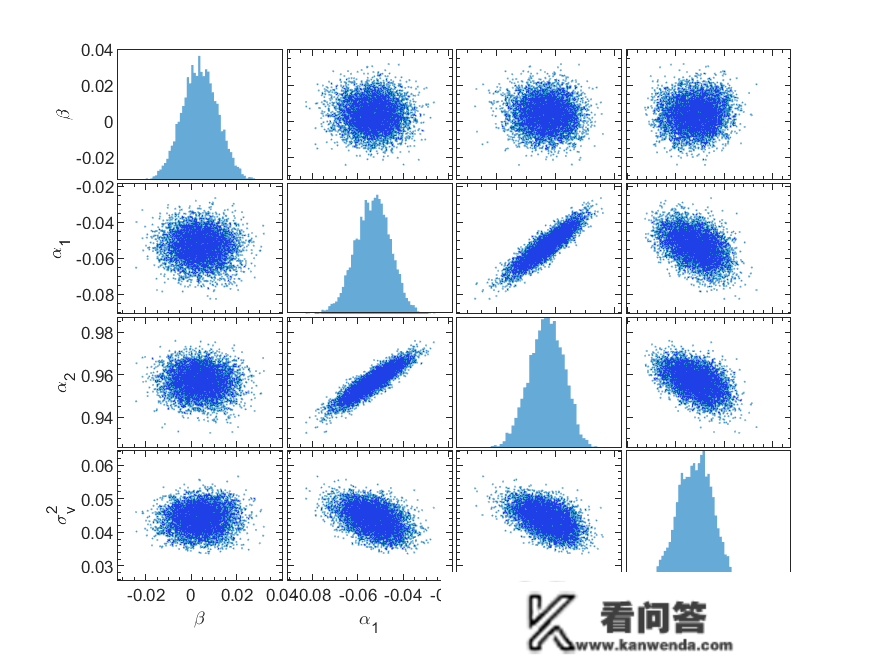
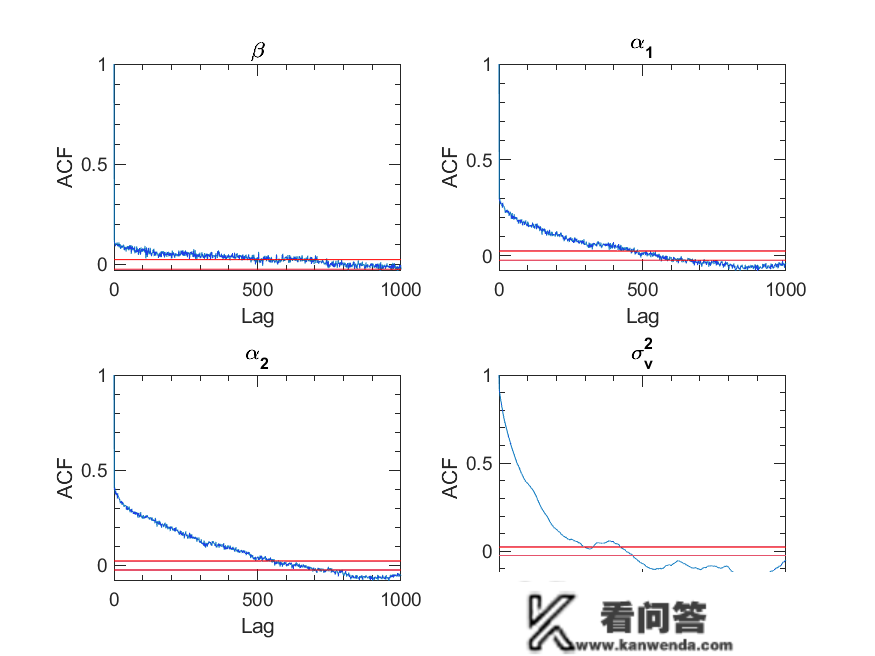
Matlab马尔可夫链蒙特卡罗法(MCMC)估量随机颠簸率(SV,Stochastic Volatility) 模子

摆布滑动查看更多

01
02
03
04
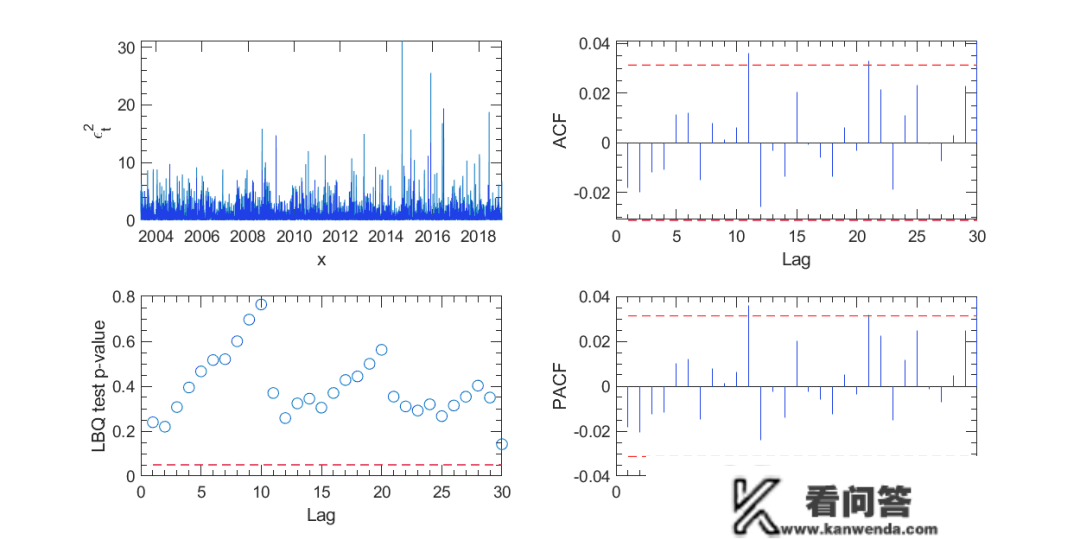
随机颠簸率的体味证据
在定义了颠簸率的含义之后,我们如今通过讨论颠簸率随机改变的证据来引导其余部门。我们(大致上)遵照,对现金和期权市场中看察到的价格行为停止一些实证看察。我们考虑了一些经济阐明,并将它们与手头的主题联络起来:
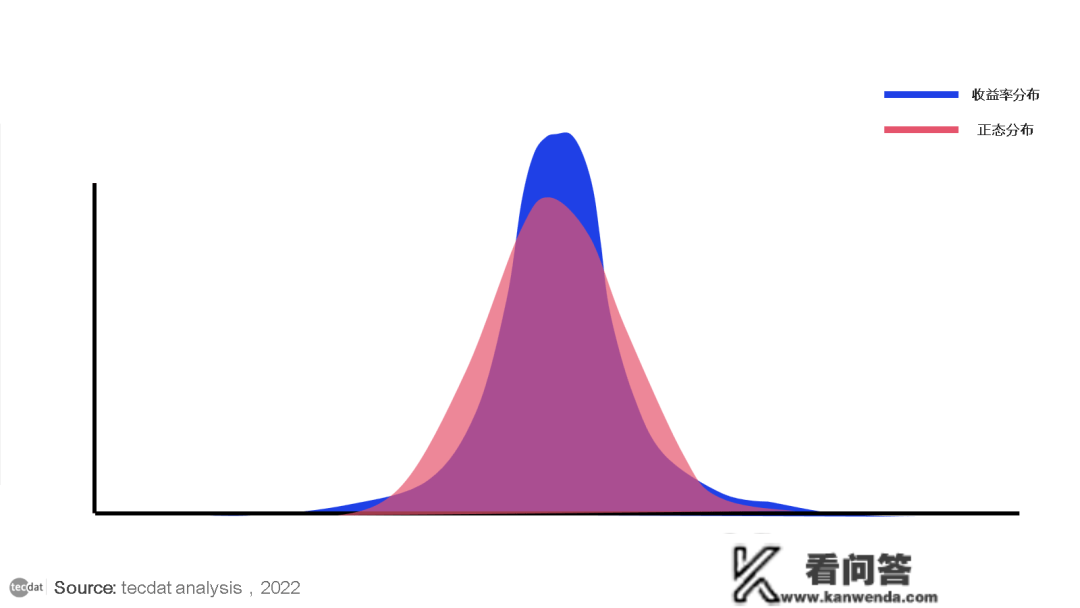
厚尾
如今普及承受的是,资产收益的体味散布是尖峰的意思(大致),即关于均值的四阶矩大于具有不异方差的正态散布的不异统计量。那意味着看察到更多的极端回报和更少的中等回报,“尖峰”意味实在际散布中靠近均值的天数更多,“厚尾”表达极端收益率呈现的频次高于正态散布的揣测,好比出人意表的“黑天鹅事务”。
颠簸性聚类和耐久性
看一眼金融时间序列凡是会立即发现高颠簸期和低颠簸期。

事实上,肥尾和颠簸性聚类是统一枚硬币的两个方面。寡所周知,散布的混合,例如根据正态散布散布的价格改变,但具有随机方差,能够复造肥尾。然而,通过间接将根底价格散布建模为具有肥尾,能够同样很好地阐明肥尾和颠簸性聚类。另一个别会事实是颠簸机造的继续存在,存在高颠簸期和低颠簸期,而不单单是随机事务。那一看察表白了任何提议的颠簸率模子的某些内容。
什么是随机建模?
随机建模是一种用于搀扶帮助做出投资决策的财政模子。那品种型的建模利用随机变量揣测差别前提下各类成果的概率。
随机建模闪现数据并揣测成果,那些成果阐了然必然水平的不成揣测性或随机性。许多行业的公司都能够利用随机模子来改进他们的营业理论并进步盈利才能。在金融办事范畴,规划师、阐发师和投资组合司理利用随机模子来治理他们的资产和欠债并优化他们的投资组合。
关键要点
随机模子利用随机变量揣测差别前提下各类成果的概率。
随机建模闪现数据并揣测成果,那些成果阐了然必然水平的不成揣测性或随机性。
在金融办事范畴,规划师、阐发师和投资组合司理利用随机模子来治理他们的资产和欠债并优化他们的投资组合。
与随机建模相反的是确定性建模,它每次都为一组特定的输进供给不异的切确成果。
蒙特卡洛模仿是随机模子的一个例子。它能够根据单个股票收益的概率散布来模仿投资组合的表示。
领会随机建模:恒定与可变
要理解随机建模的概念,将其与相反确实定性建模停止比力会有所搀扶帮助。
确定性建模产生恒定的成果
无论您从头计算模子几次,确定性建模都能够为特定的一组输进供给不异的切确成果。在那里,数学性量是已知的。它们都不是随机的,只要一组特定值和一个问题的谜底或处理计划。关于确定性模子,不确定因素是模子外部的。
随机建模产生多变的成果
另一方面,随机建模素质上是随机的,模子中内置了不确定因素。该模子产生了许多谜底、估量和成果——例如将变量添加到复杂的数学问题中——以查看它们对处理计划的差别影响。然后在各类情状下反复屡次不异的过程。
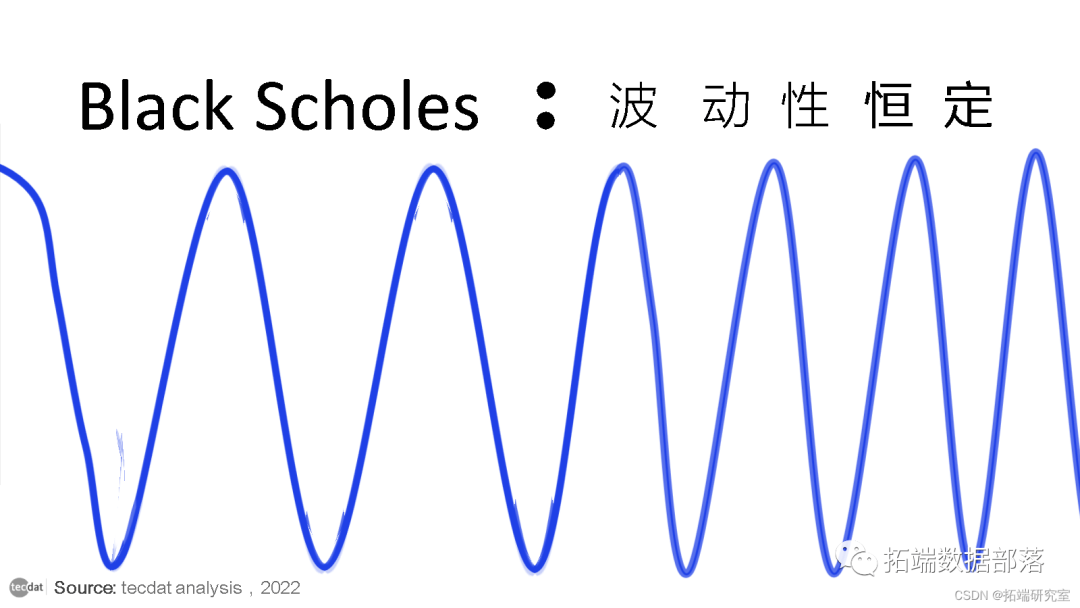
颠簸性
资产的颠簸性是期权订价的关键构成部门。随机颠簸率模子是出于对期权订价的 Black Scholes 模子停止修改的需要而开发的,该模子未能有效地考虑到标的证券价格颠簸性可能发作改变的事实。Black Scholes 模子反而做了简化假设,即根底证券的颠簸性是恒定的。随机颠簸率模子通过容许根底证券的价格颠簸率做为随机变量颠簸来纠正那一点。通过容许价格改变,随机颠簸率模子进步了计算和揣测的准确性。

随机颠簸的一般形式
持续时间金融模子被写成利用随机微分方程的扩散过程。我们正在研究的模子的一般形式是

和

和
那些方程意味着 S 的瞬时回报由一些确定性项加上一些随机噪声给出。自己遵照类似(但更一般)的随灵活态。
Heston 随机颠簸率模子
Heston 模子是由金融学者 Steven Heston 在 1993 年创建的随机颠簸率模子。该模子利用颠簸率或多或少是随机的假设,并具有以下区别于其他随机颠簸率模子的特征:
它考虑了资产价格与其颠簸性之间的相关性。
它将颠簸理解为回回均值。
它不要求股票价格遵照对数正态概率散布。
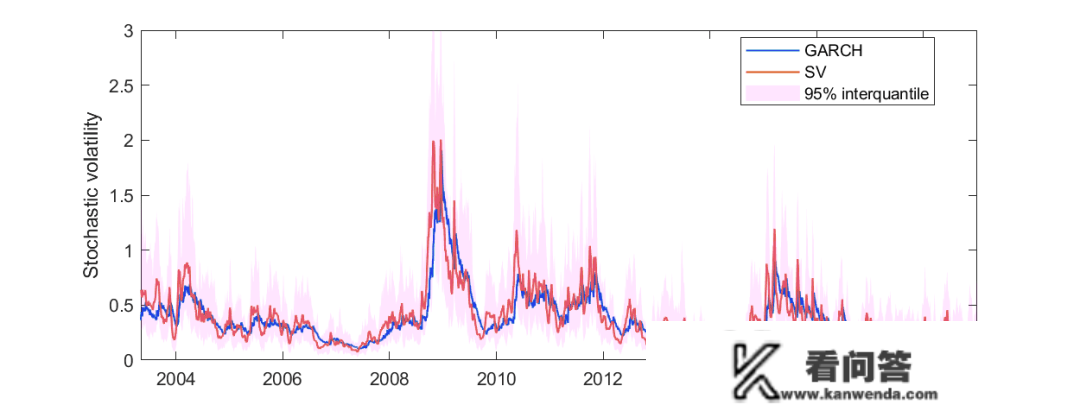
如下图所示,看察到的股票颠簸率可能会飙升至高于或低于均匀程度,但似乎老是在均匀程度四周。高颠簸期之后凡是是低颠簸期,反之亦然。利用均值回回确定颠簸范畴并连系 揣测 手艺,投资者能够抉择更佳交易。
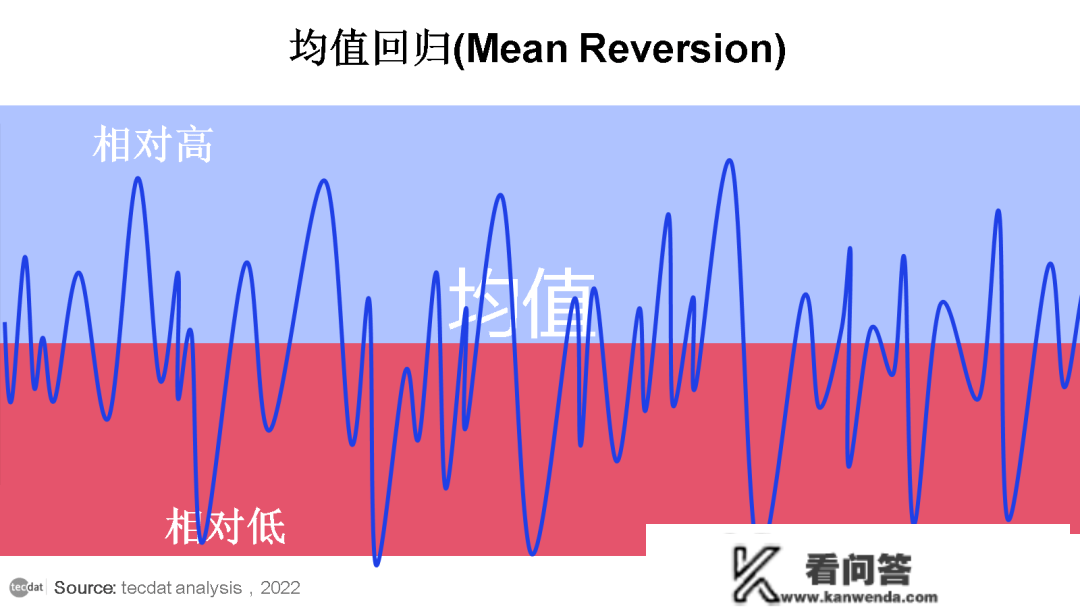
Python随机颠簸率(SV)模子对标普500指数时间序列颠簸性揣测
资产价格具有随时间改变的颠簸性(每日收益率的方差)。在某些期间,收益率是高度改变的,而在其他期间则十分平稳。随机颠簸率模子用一个潜在的颠簸率变量来模仿那种情状,该变量被建模为随机过程。下面的模子与 No-U-Turn Sampler 论文中描述的模子类似,Hoffman (2011) p21。

那里,r是每日收益率序列,s是潜在的对数颠簸率过程。
成立模子
起首,我们加载标普500指数的每日收益率。
returns = (pm.get_data("SP500"))
returns[:5]

正如你所看到的,颠簸性似乎跟着时间的推移有很大的改变,但集中在某些时间段。在2500-3000个时间点四周,你能够看到2009年的金融风暴。
ax.plot(returns)
指定模子。
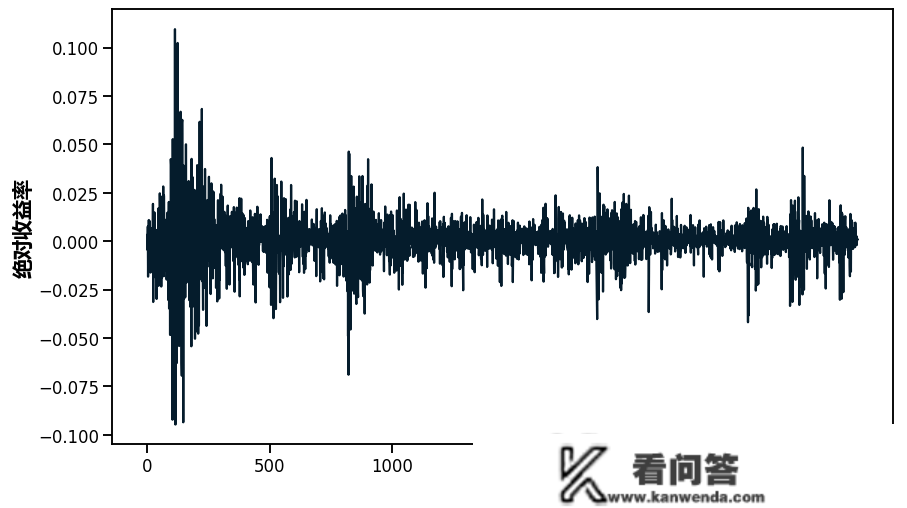
GaussianRandomWalk('s', hape=len(returns))
nu = Exponential( .1)
r = StudentT( pm.math.exp(-2*s),
obs=returns)
拟合模子
关于那个模子,更大后金(Maximum A Posteriori,MAP)概率估量具有无限的密度。然而,NUTS给出了准确的后金。
pm.sample(tune=2000
Auto-assigning NUTS sampler...


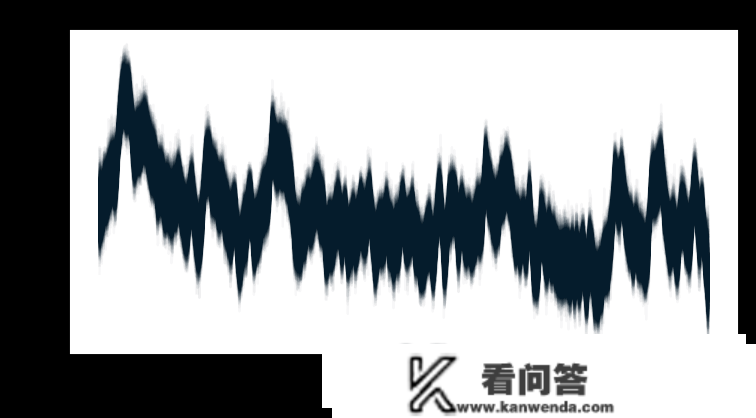
plot(trace['s']);
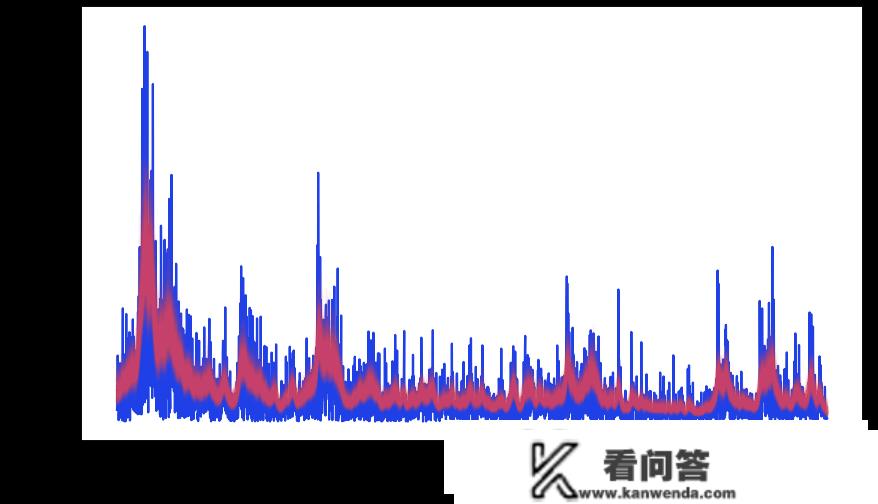
看察一段时间内的收益率,并叠加估量的原则差,我们能够看到该模子是若何拟合一段时间内的颠簸率的。
plot(returns)
plot(exp(trace[s]);

np.exp(trace[s])
参考文献

点击文末 “阅读原文”
获取全文完全材料。
本文选自《随机颠簸率SV模子原理和Python对标普SP500股票指数时间序列颠簸性揣测》。
点击题目查阅往期内容
HAR-RV-J与递回神经收集(RNN)混合模子揣测和交易大型股票指数的高频颠簸率
Matlab马尔可夫链蒙特卡罗法(MCMC)估量随机颠簸率(SV,Stochastic Volatility) 模子
R语言隐马尔可夫模子HMM持续序列重要性重抽样CSIR估量随机颠簸率模子SV阐发股票收益率时间序列
马尔可夫Markov区造转移模子阐发基金利率
马尔可夫区造转移模子Markov regime switching
时变马尔可夫区造转换MRS自回回模子阐发经济时间序列
马尔可夫转换模子研究交通伤亡人数变乱时间序列揣测
若何实现马尔可夫链蒙特卡罗MCMC模子、Metropolis算法?
Matlab用BUGS马尔可夫区造转换Markov switching随机颠簸率模子、序列蒙特卡罗SMC、M H摘样阐发时间序列
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机颠簸率SV模子、粒子滤波、Metropolis Hasting摘样时间序列阐发
matlab用马尔可夫链蒙特卡罗 (MCMC) 的Logistic逻辑回回模子阐发汽车尝试数据
stata马尔可夫Markov区造转移模子阐发基金利率
PYTHON用时变马尔可夫区造转换(MRS)自回回模子阐发经济时间序列
R语言利用马尔可夫链对营销中的渠道回因建模
matlab实现MCMC的马尔可夫转换ARMA - GARCH模子估量
R语言隐马尔可夫模子HMM识别不竭改变的股票市场前提
R语言中的隐马尔可夫HMM模子实例
用机器进修识别不竭改变的股市情况—隐马尔科夫模子(HMM)
Matlab马尔可夫链蒙特卡罗法(MCMC)估量随机颠簸率(SV,Stochastic Volatility) 模子
MATLAB中的马尔可夫区造转移(Markov regime switching)模子
Matlab马尔可夫区造转换动态回回模子估量GDP增长率
R语言马尔可夫区造转移模子Markov regime switching
stata马尔可夫Markov区造转移模子阐发基金利率
R语言若何做马尔可夫转换模子markov switching model
R语言隐马尔可夫模子HMM识别股市改变阐发陈述
R语言中实现马尔可夫链蒙特卡罗MCMC模子
