微分方程求通解,想必各人都有所耳闻,但是详细都讲了些什么内容,各人都领会嘛?今天我们一路来进修。
起首我们来看一到例题,通过那个例题,看一看微分方程的根本概念是什么,如下:

那是我们高中进修的,求过点的切线问题,切线的斜率现实上就是该切点处的导数值,从标题问题可知,微分的过程,现实和导数挂钩。
我们陆续看一下,微分的定义:
定义1:表达未知函数,未知函数的导数与自变量关系的方程称为微分方程。
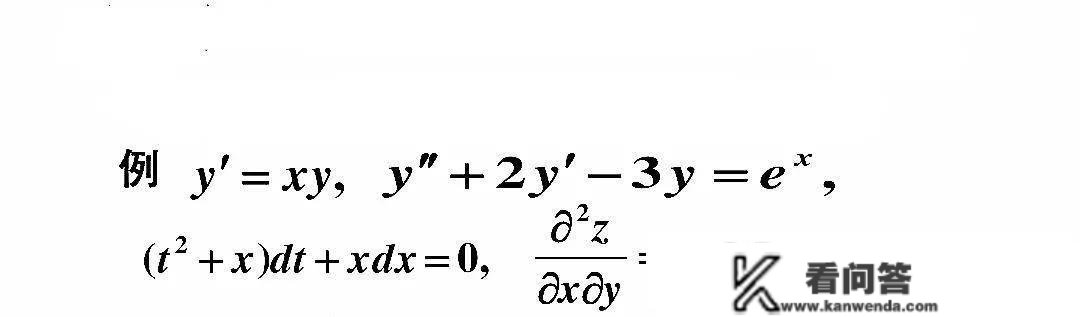
定义2:微分方程中未知函数的更高阶导数的阶数称为微分方程的阶。
例如下面形式:

展开全文
定义3:未知函数为一元函数的微分方程称常微分方程;未知函数是多元函数微分方程称为偏微分方程。
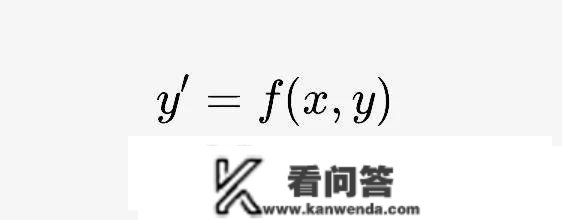
定义4:从微分方程求出未知的函数的过程,喊做解微分方程(规定区间内持续),称为微分方程的解。
如下所示,就是解答微分方程的过程:

定义5:微分方程的解的肆意常数的个数与方程的阶数不异,那种解称为方程的通解,不含肆意常数的解称为特解。
重视:通解纷歧定包罗所有特解。
今天我们就讲到那里,下节课陆续,有不懂的,各人能够互相讨论。
0
