“利用符号,是数学史上的一件大事。一套适宜的符号,绝不单单是起速记、节约时间的感化。它可以切确、深入地表达某种概念、办法和逻辑关系。一个较复杂的公式,假设不消符号而用日常语言来论述,往往非常冗长并且模糊不清。”(引自我国数学史家梁宗巨的《世界数学史简编》)。
1 积分符号∫的由来
积分的素质是无限小的和,拉丁文中“Summa”表达“和”的意思。将“Summa”的头一个字母“S”拉长就是∫。
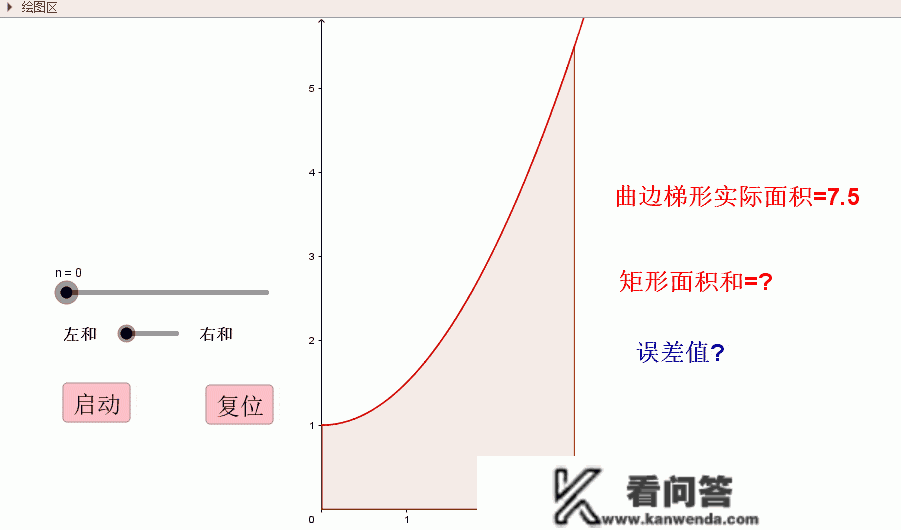
创造那个符号的人是德国数学家莱布尼茨(Friedrich , Leibniz)。莱布尼兹具有渊博的常识,在数学史上他是最伟大的符号学者,而且具有符号巨匠的佳誉。莱布尼兹曾说:“要创造,就要挑选安妥的符号,要做到那一点,就要用含义简明的少量符号来表达和比力忠实地描画事物的内在素质,从而更大限度地削减人的思维劳动。”莱布尼兹创设了积分、微分符号,以及商“a/b”,比“a:b”,类似“∽”,全等“≌”,并“∪”,交“∩”等符号。
牛顿和莱布尼茨在微积分方面都做出了浩荡奉献,只是两者在抉择的办法和路子方面存在必然的差别。在研究力学的根底上,牛顿操纵几何的办法对微积分停止研究;在对曲线的切线和面积的问题停止研究的过程中,莱布尼兹摘用阐发学办法,同时引进微积分要领。在研究微积分详细内容的先后挨次方面,牛顿是先有导数概念,后有积分概念;莱布尼兹是先有求积概念,后有导数概念。在微积分的利用方面,牛顿足够连系了运动学,而且造诣较深;而莱布尼兹则逃求简洁与准确。
展开全文
别的,牛顿与莱布尼兹在学风方面也迥然差别。牛顿做为科学家,具有严谨的治学风气。牛顿迟迟没有颁发他的微积分著做《流数术》的原因,次要是他没有找到科学、合理的逻辑根底,别的,可能也是担忧他人的反对。与此相反,莱布尼兹做为哲学家,富于想象,比力斗胆,勇于妥帖,次要表示为,在创做年代方面:牛顿比莱布尼兹领先10年,然而在颁发时间方面,莱布尼兹却领先牛顿3年。关于微积分的研究,固然牛顿和莱布尼兹摘用的办法差别,但是却殊途同回,而且各自完成了创建微积分的盛业。
2 无限大符号∞的由来
将8程度置放成“∞”来表达“无限大”符号。
有人说那个符号的创意来自莫比乌斯带,因为假设某小我站在一个浩荡的莫比乌斯带的外表上沿着他能看到的“路”不断走下往,他就永久不会停下来。但有人辩驳说“∞”的创造比莫比乌斯带还要早。

罗马人将“∞”表达为1000,后来用于表达肆意的十分大的数,无限大。牛津大学的传授约翰·威廉在公元1665年之一次将那个符号表达为无限。但该符号曲至1713年贝努利利用它之后,才被广为摘纳。
3 极限符号lim的由来
“极限”一词源于拉丁文“limes”,缩写为“lim”。1786年瑞士数学家鲁易理(Lhuillier)初次引进,后人不竭完美,开展了长达122年之久,由英国数学家哈代(Haddy)的完美极限符号才成为今天通用的符号。
4 天然对数底数符号e的由来
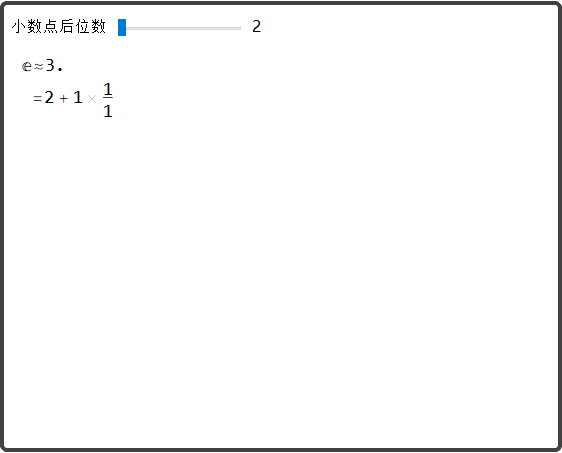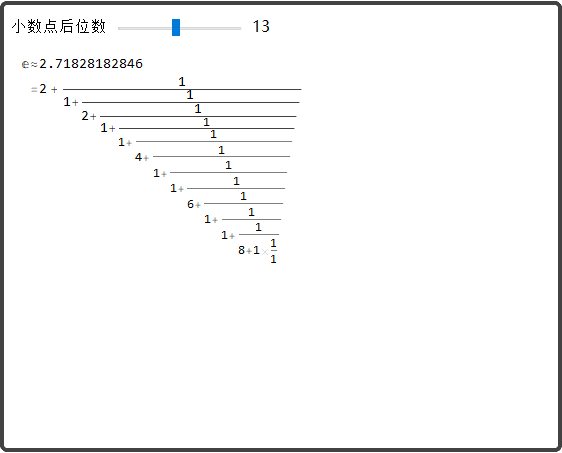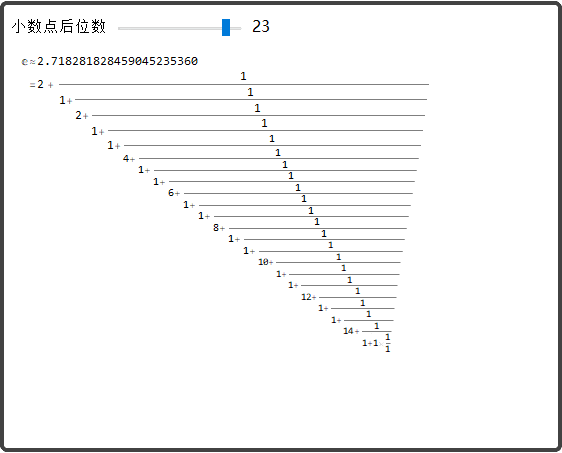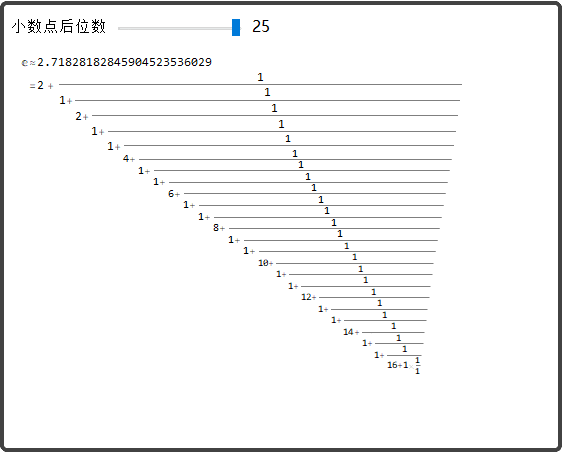
就像圆周率π和虚数单元i,e是数学中最重要的常数之一,是瑞士数学家及天然科学家欧拉(Euler)发现的,它是个无限不轮回小数,其值等于2.71828……以e为底的对数喊做天然对数,用符号“ln”表达。求极限e的公式被英国科学期刊《物理世界》2004年10月号公布为读者选出的科学界历来“最伟大的公式”之一,而且名列第二。
在父亲的教导下,欧拉13岁进进巴塞尔大学,15岁大学结业,16岁获得硕士学位。在一场沉痾中,他的左眼完全失明,凭仗惊人的记忆力和默算身手,欧拉陆续科学创做,他与助手们通过讨论或者间接口授的体例完成大量的科学著做。欧拉在18世纪的数学界做为最出色的人物,为数学界做出出色的奉献,同时将数学推至几乎整个物理的范畴。别的,欧拉还创设了许大都学符号,此中他将曲面表达为z=f(x,y)并引进一系列原则符号以表达z对x,y的偏导数,至今那些符号仍通用。欧拉对数学的研究如斯普遍,因而以他的名字定名的重要常数、公式和定理等在许大都学的分收中也可经常见到。
5 数集符号由来
天然数集N、整数集Z、有理数集Q、实数集R,复数集C是别离由单词natural number(英语“天然数”的意思)、Zahlen(德语“整数”的意思,一位德国数学家在整数环中初次用那个字母,后来被沿用)、quotient(英语“商”的意思,因为有理数是两个整数比拟的成果,有理数的英文是rational number,但假设取头一个字母就会和实数集符号相重)、real number(英语“实数”的意思)、complex number(英语“复数”的意思)。
6 属于符号∈的由来
“∈”表达一个元素属于某一聚集的记号,是意大利数学学家皮亚诺(Peano)在1889年的数学著做中起首利用的。
在数系理论研究方面,皮亚诺做出了严重奉献。在1889年出书的《算术原理新办法》一书中,皮亚诺提出 “皮亚诺天然数公理”举世闻名,在书中他还对许多逻辑符号停止了立异。在1891年创建了《数学杂志》,皮亚诺在那个杂志上操纵数理逻辑符号写下天然数公理,并对它们的独立性停止了证明。皮亚诺于1893年颁发《无限小阐发教程》,该书被德国的数学百科全书列在“自L.欧拉(Euler)和A.L,柯西(GAUCHY)时代以来最重要的19本微积分教科书”之中。皮亚诺撰写的《数学百科全书》中有良多处所有目共睹,例如妥帖微分中值定理;多变量函数一致持续性的断定定理;隐函数存在定理以及其可微性定理的证明;部门可微但整体不成微的函数的例子;其时时髦的极小理论的反例等。
7 平方根符号的由来
“根”的拉丁语是radix,它是 *** 语的译名,在数学上具有双重意义;一方面表达方程的未知数,另一方面又表达一个数的平方根。1637年,法国哲学家、数学家笛卡尔在光辉的《几何学》著做中,他巧妙地在路多尔夫、斯蒂文创用的符号“√”上面添上一个括线“—”,即用根号表达平方根(且多了一个小钩)。

将代数和几何巧妙地联络在一路,那是笛卡尔在数学上的出色奉献,从而创造领会析几何那门学科。笛卡尔于1760年2月,病逝于斯德哥尔摩,因为教会的阻遏,为其送葬仅有几个友人。在他身后其著做也被教会列为禁书。但是,广阔科学家和革命者却对那位对科学做出浩荡奉献的学者充满了敬重和驰念。笛卡尔的骨灰和遗物在法国大革命之后被送进法国汗青博物馆。其骨灰在1819年被移进圣日耳曼圣心堂中。墓碑上镌刻着:笛卡尔,欧洲文艺复兴以来,之一个为争取和保卫理性权力而斗争的人。
来自:数学与通识
