讲机率、论统计数据，确实要从抛银币讲起啊，那才是得当关上坐姿嘛。
1 甚么是形态参数？
你说你的银币是公平的，也是“花”和“字”再次呈现的机率是相差无几的。
接着，你想和我赌，做为两个现职的偏执江湖术士，我怎能轻信你的回禀，我明白提出要查抄和下你的银币到底呢公平的，如果是两边“花”咋办？影片里面并不是经常再次呈现如许的戏码？
你神气亢奋，非要不准我查抄和，后来他们明白提出了折中的计划，抛数次银币，看看结论呢公平的。
一共扔了三次，都是“花”朝上，固然机率是 0.5\times 0.5=0.25 ，但也恒定，竭尽全力扔。
一共扔了三次，也都是“花”朝上，机率是 0.5^4=0.0625 ，觉得有点不恒定，但如果是临场阐扬呢？竭尽全力扔。
一共扔了七次，也都是“花”朝上，那我就指出很可能将你那枚银币并不是公平的。
那是形态参数：
你明白提出假定：说你的银币是公平的我明白提出要检测你的假定：扔七次，看试验的结论呢和你的假定相符合2 P值
为了完成形态参数，需要先表述两个根本概念：P值。他们那儿就来申明甚么是P值？
按照下面的论述，那儿形态参数的路子是：
假定：银币是公平的检测：指出假定是成立的，接着扔七次，看结论与假定能否相符合反频频复扔银币若是符合概率密度函数（那就不申明了），也是：
X\sim B(n,\mu )\\
此中， n 代表者扔银币的单次， \mu 代表者“花”朝上的机率。
在他们指出银币是公平的大前提下，扔10次银币若是符合以下散布：
X\sim B(10, 0.5)\\
右图暗示的是，假使银币是公平的情况下的示企图：
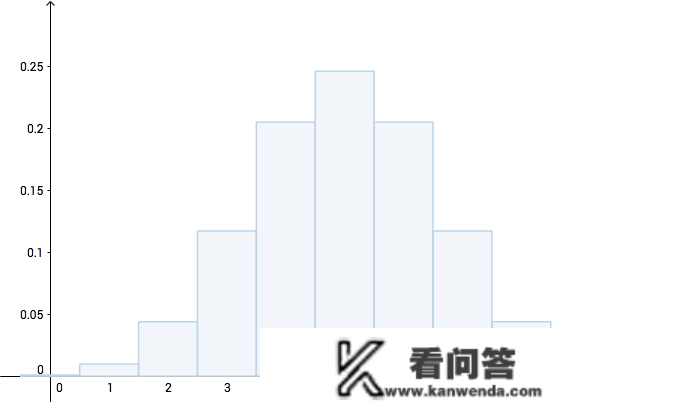
我扔了七次之后获得的结论是，有六次背面：
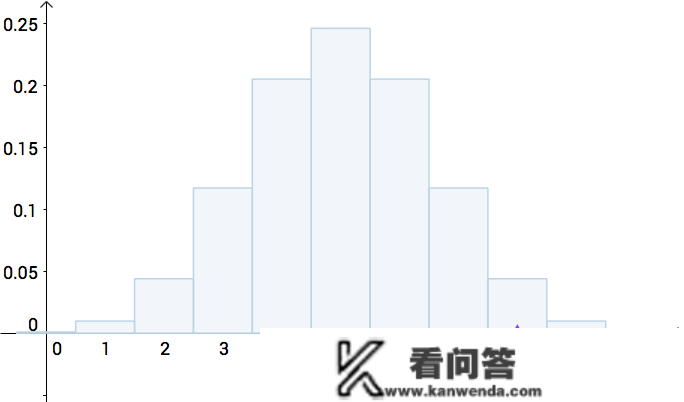
阿谁时候有位微积分元老出来表述了两个称为 P 值（p-value)的根本概念：
杰弗里·Haveri·鲍威尔查理斯（1890－1962）把六次背面的机率，与更顽固的六次背面、七次背面的机率加出来：
获得的是（双侧P值）：
\text {p-value}=P(8\leq X\leq 10)=0.05\\
其实，再次呈现三次背面、一次背面、ii背面的机率也是很顽固的：
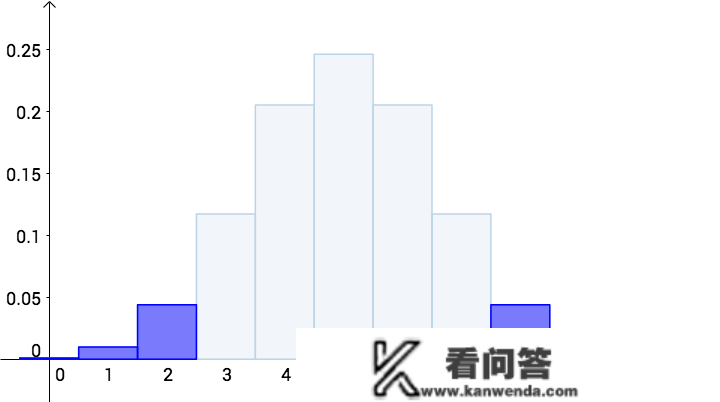
所以（双侧P值）：
\text {p-value}=P(0\leq X\leq 2)+P(8\leq X\leq 10)=0.1\\
2.1 为甚么要把更顽固的情况加出来？
按照扔银币阿谁规范，可能将你会觉得，我晓得六次背面再次呈现不恒定就行了，干嘛要把六次、七次加出来？
我觉得有那么两个现实原因，好比我要扔1000次银币来测试假定能否得当。
扔1000次银币用概率密度函数来计算很费事，按照中心极限制理，他们晓得，能够用正态散布来近似：
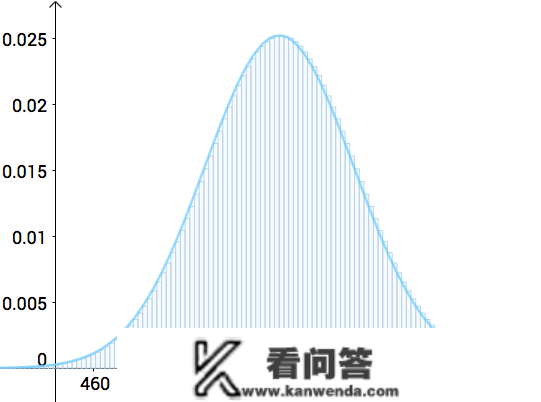
好比，我扔了1000次，获得了530次背面，用正态散布来计算就比力简单。
但，关于正态散布，我没有法子算单点的机率（持续散布单点机率为0），我只能取两个区间来算极限，所以就取530、以及更顽固的点构成的区间：
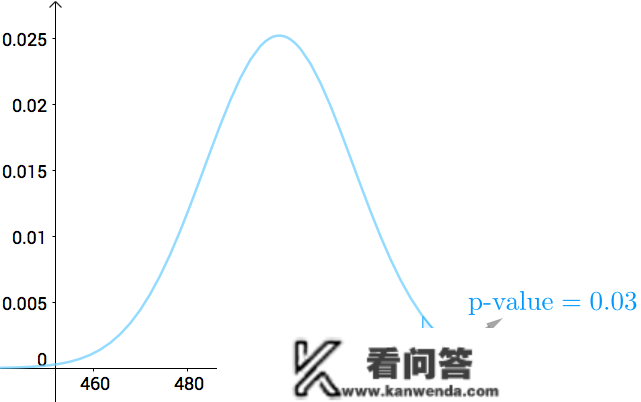
我下面只取了双侧P值，申明下：
取双侧仍是双侧，取决于你的应用甚么叫做更顽固的点，也取决于你的应用3 显著程度
一共扔10次银币，那么是再次呈现7次背面之后，能够指出“银币是不公平的”，仍是9次背面之后我才气确认“银币是不公平的”，那是两个较为主不雅的尺度。
他们一般指出
\text {p-value}\leq 0.05\\
就能够指出假定是不得当的。
0.05阿谁尺度是显著程度，当然选择几做为显著程度也是主不雅的。
好比，下面的扔银币的规范，若是取双侧P值，那么按照他们的计算，若是扔10次再次呈现9次背面：
\text {p-value}=P(9\leq X\leq 10)=0.01\leq 0.05\\
暗示出来如右图所示：
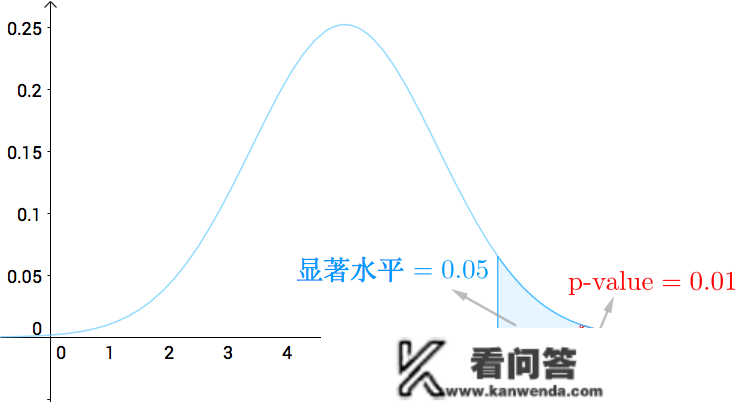
他们能够指出刚起头的假定错的很“显著”，也是“银币是不公平的”。
若是扔10次再次呈现再次呈现8次背面：
\text {p-value}=P(8\leq X\leq 10)=0.05\leq 0.05\\
呃，阿谁和他们的显著程度是一样的啊，他们也能够回绝假定，只是没有那么“显著”了。
4 与置信区间的关系
常识要联络出来看，理解更深入。
置信区间，目标是按照样本构造两个区间，接着希望阿谁区间能够把实值包罗进去，但其实不晓得阿谁实值是几？详细能够参考 若何理解 95% 置信区间？
而形态参数，则是假定实值是几，接着检测阿谁假定能否可能将为实。
之所以觉得它们有关系，大要是因为它们都提到了0.05。
它们之间的关系也简单，若是他们明白提出来的假定 \mu _0 在样本 \bar{x} 的置信区间内，就能够通过测试：
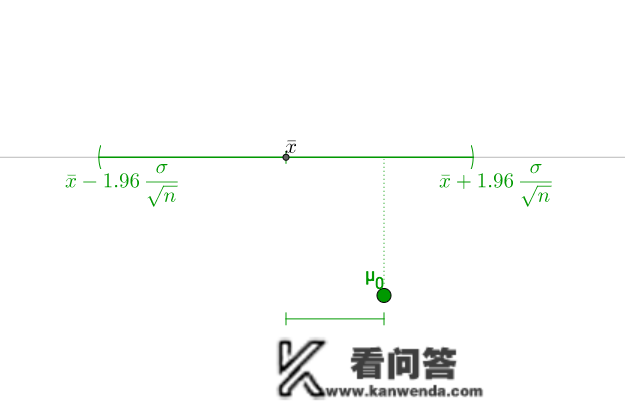
反之，就不克不及通过：
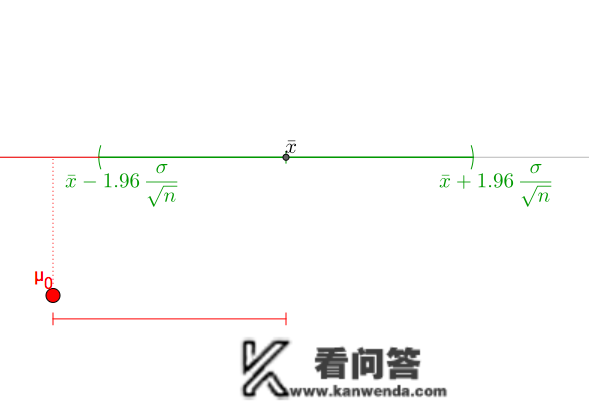
更多内容保举马同窗图解微积分系列教程
《马同窗图解线性代数》笼盖大学公共课内容
天猫
¥69.00
去购置
《马同窗图解线性代数》彩印线拆！天然微积分TOP1
京东
¥69.00
去购置
马同窗图解微积分（都雅易懂！2万名同窗参加进修）
淘宝
¥99.00
去购置