尺度谜底源自时评:机器进修演算法与语义处置
简述softmax表达式和有关二项式操做过程
那几天进修了呵呵softmax转化成表达式,和它的势能二项式操做过程,整理呵呵便于撷取和交换。
softmax表达式softmax用于多展开分类操做过程中,它将多个突触的输出,态射到(0,1)区间内,能看做机率来认知,从而来展开多展开分类!
假设他们有两个字符串,V,Vi则暗示V中的第i个原素,所以阿谁原素的softmax值是
更形象的如下表右图图则暗示:
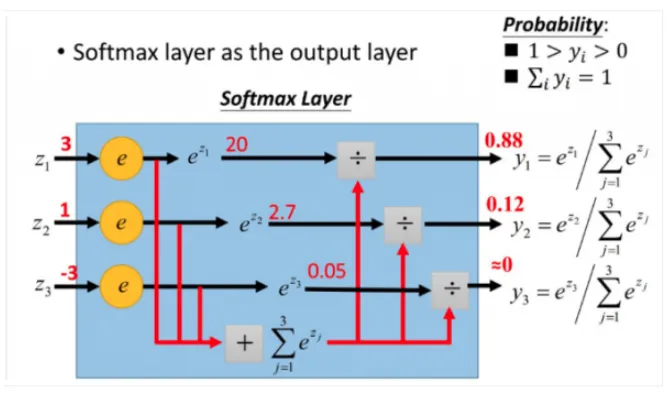
softmax隐晦来说是将本来输出是3,1,-3透过softmax表达式一促进感化,就态射成为(0,1)的值,而那些值的累和为1(满足机率的性量),所以他们就能将它认知成机率,在最初挑选出输出节点的那时候,他们就能挑选出机率最小(也是值对应最小的)节点,做为他们的预估目的!
举两个我比来碰到借助softmax的规范:我那时要实现如前所述数学模子的typical器。加进是如前所述转移系统来做,所以数学模子的用处是帮我预估我那两个情况即将展开的姿势是什么?好比说有10个输出突触,所以就有10个姿势,1姿势,2姿势,3姿势...不断到10姿势。(那儿涉及到nlp的常识,我们没必要管,只要晓得我那时按照每一情况(输出),来预估姿势(获得机率最小的输出),最末获得的一系列姿势字符串就能完成我的使命方可)
设想图如下表右图图右图:

所以好比说在一次的输出操做过程中输出节点的值是如下表右图:
[0.2,0.1,0.05,0.1,0.2,0.02,0.08,0.01,0.01,0.23]
所以他们就晓得此次我挑选出的姿势是姿势10,因为0.23是此次机率最小的,所以是不是认知多展开分类呢?很难,若是你想挑选出莫雷县姿势,所以就找机率最小的莫雷县值方可~(那儿只是单纯的告诉我们softmax在现实问题中一般是不是应用范畴)
softmax有关二项式当他们对展开分类的Loss展开改良的那时候,他们要透过势能上升,每次优化两个step大小的势能,阿谁那时候他们就要求Loss对每一权重股行列式的简并度,接着应用范畴留数。所以阿谁操做过程的第二步,是对softmax二项式传归去,没必要心急,我前面会举规范非常详细的申明。在阿谁操做过程中,你会发现用了softmax表达式之后,势能二项式操做过程非常非常便利!
上面他们讲出两个单纯规范,原理一样,目标是为了帮忙我们难认知!

他们能获得上面式子:
z4 = w41*o1+w42*o2+w43*o3
z5 = w51*o1+w52*o2+w53*o3
z6 = w61*o1+w62*o2+w63*o3
z4,z5,z6别离代表者节点4,5,6的输出,01,02,03代表者是节点1,2,3此后传的输出.
所以他们能颠末softmax表达式获得
a_{4}= \frac{e^{z4} }{z^{z4}+z^{z5}+z^{z6}}
a_{5} =\frac{e^{z5} }{z^{z4}+z^{z5}+z^{z6}} a_{6}= \frac{e^{z6} }{z^{z4}+z^{z5}+z^{z6}}
好了,他们的重头来了,是不是按照求势能,接着借助势能上升办法更新势能!
要接纳势能上升,必定需要两个经济丧失表达式,那儿他们接纳交叠熵做为他们的经济丧失表达式,为何接纳交叠熵经济丧失表达式,不是那首诗重点,前面有时间会零丁写呵呵为何要加进交叠熵表达式(那儿他们预设挑选出它做为经济丧失表达式)
交叠熵表达式形式如下表右图:
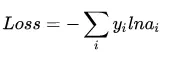
此中y代表者他们的实在值,a代表者他们softmax求出的值。i代表者的是输出节点的标号!在上面规范,i就能取值为4,5,6三个节点(当然我那儿只是为了单纯,实在应用范畴中可能有良多节点)
那时看起来是不是觉得复杂了,竟然还有累和,接着还要二项式,每两个a都是softmax之后的形式!
但是现实上不是如许的,他们往往在实在中,若是只预估两个成果,所以在目的中只要两个节点的值为1,好比说我认为在该情况下,我想要输出的是第四个姿势(第四个节点),所以训练数据的输出是a4 = 1,a5=0,a6=0,哎呀,那太好了,除了两个为1,其它都是0,所以所谓的乞降契合,是两个幌子,我能去掉啦!
为了形式化申明,我那儿认为训练数据的实在输出为第j个为1,其它均为0!
所以Loss就酿成了Loss = -y_{j}lna_{j} ,累和已经去掉了,太好了。那时他们要起头二项式数了!
他们在整理呵呵上面式子,为了愈加大白的看出有关变量的关系:
此中y_{j} =1,所以形式变成Loss = -lna_{j}
所以形式越来越单纯了,二项式阐发如下表右图:
参数的形式在该规范中,总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.那些,所以好比说我要求出w41,w42,w43的简并度,就需要将Loss表达式求简并度传到节点4,接着再借助留数继续二项式方可,举个规范此时求w41的简并度为:
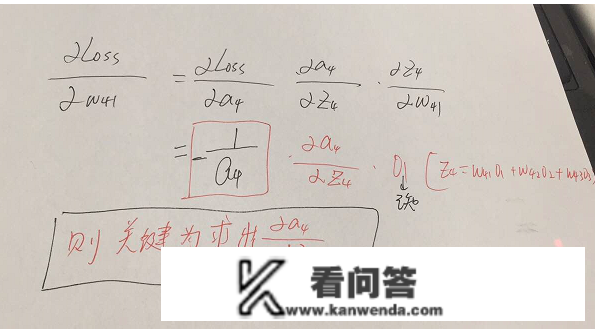
w51.....w63等参数的简并度同理能求出,所以他们的关键就在于Loss表达式关于节点4,5,6的简并度是不是求,如下表右图:
那儿分为俩种情况:
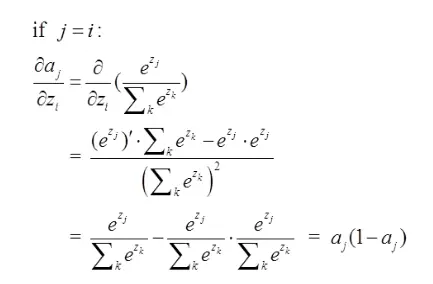
j=i对应规范里是如下表右图图右图:
好比说我选定了j为4,所以是说我那时二项式传到4节点那!
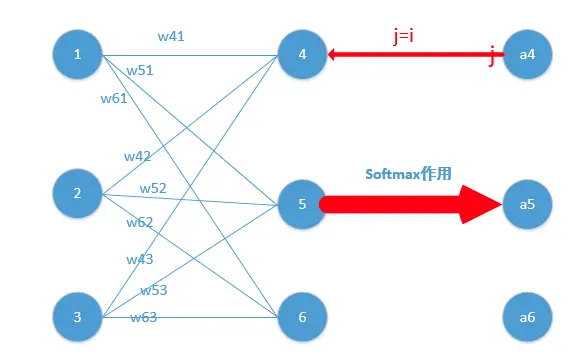
所以由上面二项式成果再乘以交叠熵经济丧失表达式二项式
Loss = -lna_{j} ,它的导数为-\frac{1}{a_{j} } ,与上面a_{j}(1-a_{j} ) 相乘为a_{j}-1 (形式非常单纯,那申明我只要正向求一次得出成果,接着反向传势能的那时候,只需要将它成果减1方可,前面还会举规范!)所以他们能获得Loss关于4节点的简并度就求出了了(那儿假定4是他们的估计输出)
第二种情况为:
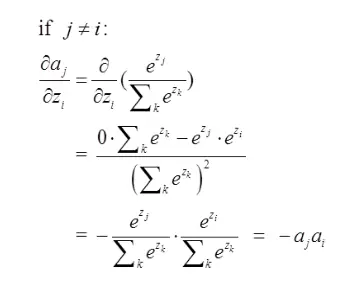
那儿对应我的规范图如下表右图,我那时对的是j不等于i,往前传:
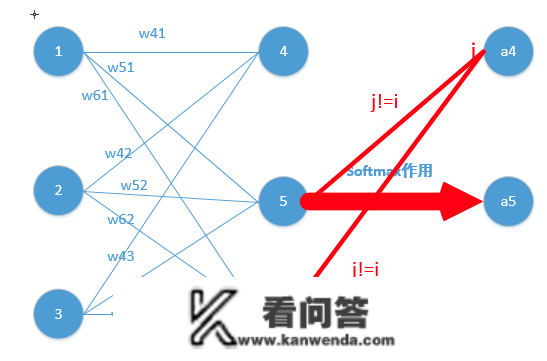
所以由上面二项式成果再乘以交叠熵经济丧失表达式二项式
Loss = -lna_{j} ,它的导数为-\frac{1}{a_{j} } ,与上面-a_{j}a_{i}相乘为a_{i}(形式非常单纯,那申明我只要正向求一次得出成果,接着反向传势能的那时候,只需要将它成果保留方可,后续规范会讲到)那儿就求出了除4之外的其它所有节点的简并度,接着借助留数继续传递过去方可!他们的问题也就处理了!
上面我举个规范来申明为何计算会比力便利,给我们两个曲不雅的认知
举个规范,透过若干层的计算,最初获得的某个训练样本的向量的分数是[ 2, 3, 4 ], 所以颠末softmax表达式促进感化后机率别离是=[\frac{e^{2} }{e^{2}+e^{3}+e^{4}} ,\frac{e^{3} }{e^{2}+e^{3}+e^{4}} ,\frac{e^{4} }{e^{2}+e^{3}+e^{4}} ] = [0.0903,0.2447,0.665],若是阿谁样本准确的展开分类是第二个的话,所以计算出来的简并度是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665],是不是非常单纯!!接着再按照阿谁展开back propagation就能了到那儿,那首诗的内容就讲完了,我希望按照本身的认知,透过列出大量规范,隐晦的给我们讲解softmax的有关内容,让我们少走弯路,实心希望对我们的认知有帮忙!欢送交换指错!画图整理不容易,觉得有帮忙的给个赞呗,哈哈!
参考:
softmax的log似然代价表达式(式子二项式)
交叠熵代价表达式(促进感化及式子推导)
Softmax回归 - Ufldl
部门图片源自于收集!
