高中复数数学公式?
(a+bi)+(c+di)=(a+c)+(b+d)i、z1+z2=z2+z1、(z1+z2)+z3=z1+(z2+z3)等。
复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受,而复数域是实数域的代数闭包,即任何复系数多项式在复数域中总有根。
关注
复数的四则运算公式:
加减法运算:(a+bi)±(c+di)=(a±c)+(b±d)i
乘法运算:(a+bi)(c+di)=(ac-bd)+(bc+ad)i
除法运算:(c+di)(x+yi)=(a+bi)
了解复数的运算公式之前,应该先明白复数的定义,在定义的基础上理解、运用复数的运算公式。今天小柒老师给众人详细的讲解一下中学复数的运算公式。
一、复数的定义
复数是形如a+bi的数。式中a,b为实数,i是一个满足i=-1的数,由于任何实数的平方不等于-1,因此i不是实数,而是实数以外的新的数。在复数a+bi中,a称为复数的实部,b称为复数的虚部,i称为虚数单位。当虚部等于零时,这个复数就是实数;当虚部不等于零时,这个复数称为虚数,虚数的实部如果等于零,则称为纯虚数。由上可知,复数集包含了实数集,因而是实数集的扩张。复数常用形式z=a+bi叫做代数式。

二、复数的四则运算公式
加减法运算 设z1=a+bi,z2=c+di是任意两个复数,它的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和:(a+bi)±(c+di)=(a±c)+(b±d)i。
乘法运算 设z1=a+bi,z2=c+di是任意两个复数,则:(a+bi)(c+di)=(ac-bd)+(bc+ad)i。其实就是把两个复数相乘,类似两个多项式相乘,结果中i=-1,把实部与虚部分别合并。两个复数的积仍然是一个复数。
除法运算 复数除法定义:满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。
运算 *** :可以把除法换算成乘法做,将分子分母同时乘上分母的共轭复数,再 用乘法运算。
例:求(a+bi)/(c+di)
我们设结果为x+yi
只需解方程(a+bi)=(c+di)(x+yi)即可
也就是方程组cx-dy=a cy+dx=b
解得x=(ac+ba)/(c+d) y=(bc-ad)/(c+d)
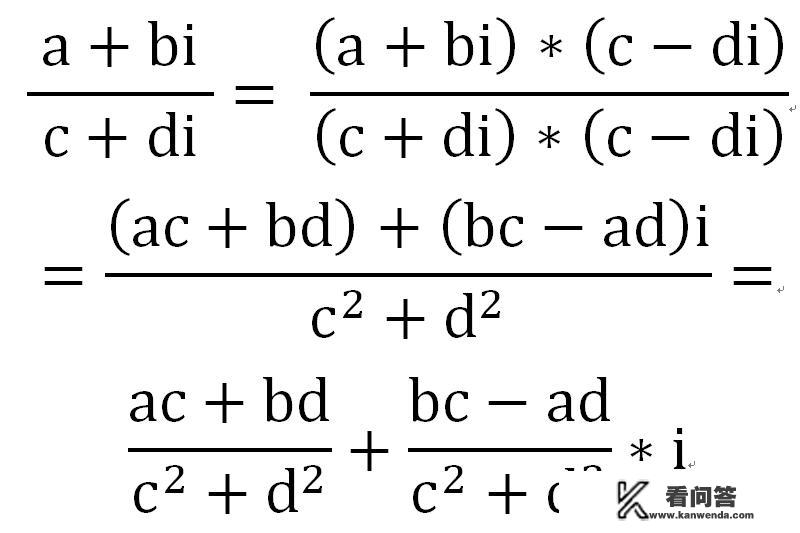
谁有高中数学关于复数的公式?
1. 复数的定义:形如$a+bi$($i$为虚数单位,$a,b$为实数)的数称为复数,其中$a$称为复数的实部,$b$称为复数的虚部,用$\mathrm{Re}(z)$表示实部,用$\mathrm{Im}(z)$表示虚部,即$z=a+bi=\mathrm{Re}(z)+\mathrm{Im}(z)i$。
2. 纯虚数的定义:虚部为非零数的复数称为纯虚数。
3. 共轭复数的定义:复数$z=a+bi$的共轭复数定义为$\bar{z}=a-bi$,其中$\bar{z}$表示$z$的共轭复数。
4. 模长的定义:复数$z=a+bi$的模长定义为$|z|=\sqrt{a^2+b^2}$。
5. 幅角的定义:复数$z=a+bi$在复平面上对应的角度$\theta$称为幅角,其中$\theta$满足$\sin{\theta}=\dfrac{b}{|z|}$,$\cos{\theta}=\dfrac{a}{|z|}$。
6. 欧拉公式:$e^{ix}=\cos{x}+i\sin{x}$,其中$x$为实数。
7. 极就座标形式:对于一个复数$z$,可以将其表示为$z=r(\cos{\theta}+i\sin{\theta})$的形式,其中$r=|z|$为模长,$\theta$为幅角。
8. 复数的加法和减法:设$z_1=a_1+b_1i,z_2=a_2+b_2i$,则$z_1+z_2=(a_1+a_2)+(b_1+b_2)i$,$z_1-z_2=(a_1-a_2)+(b_1-b_2)i$。
9. 复数的乘法:设$z_1=a_1+b_1i,z_2=a_2+b_2i$,则$z_1z_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i$。
10. 复数的除法:设$z_1=a_1+b_1i,z_2=a_2+b_2i$,则$\dfrac{z_1}{z_2}=\dfrac{a_1a_2+b_1b_2}{a_2^2+b_2^2}+\dfrac{a_2b_1-a_1b_2}{a_2^2+b_2^2}i$。
11. 直角就座标系下的复数表示:实部为$x$,虚部为$y$的复数表示为$x+yi$。
12. 极就座标系下的复数表示:模长为$r$,幅角为$\theta$的复数表示为$r(\cos{\theta}+i\sin{\theta})$。
1. 复数的模长公式:|z|=√(a²+b²)。
复数的幅角公式:θ= arctan(b/a)。
2. 高中数学学到复数时,学生会学到到这些公式,其中模长公式是用来求复数的大小的,幅角公式是用来求复数的方向的。
此外,还有复数的加减、乘除等基本运算规则,以及楚费罗斯定理、欧拉公式等高阶知识。
复数的应用非常广泛,尤其在物理、电子、通信等领域有重要应用。
